题目内容

10．已知函数f（x）=x3-ax2+4的零点小于3个，则a的取值范围是（　　）
A．（-∞，0]B．（-∞，1]C．（-∞，2]D．（-∞，3]

分析 求出函数的导数，通过a的符号，求解函数的极值，判断函数的零点个数．

解答 解：f′（x）=3x2-2ax=3x（x-$\frac{2a}{3}$），
当a＜0时，f（x）在x=$\frac{2a}{3}$处取得极大值f（$\frac{2a}{3}$）=4-$\frac{4}{27}$a3＞0，
在x=0处取得极小值f（0）=4＞0，此时有一个零点，满足条件；
当a=0时显然满足条件，
当a＞0时，在x=0处取得极大值4，在x=$\frac{2a}{3}$处取得极小值4-$\frac{4}{27}$a3≥0，
解得a≤3，
故选：D．

点评 本题考查函数的导数的综合应用，函数的极值以及函数的零点个数的关系，考查分类讨论思想以及转化思想的应用，考查计算能力．

练习册系列答案
相关题目
20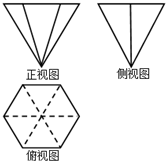．一个几何体的三视图如图所示，其中正视图是边长为2的等边三角形，俯视图为正六边形，则该几何体的侧视图的面积是（　　）
A．2B．1C．$\frac{1}{2}$D．$\frac{3}{2}$
1．如图所示，在四面体中，若直线EF和GH相交，则它们的交点一定（　　）
A．在直线DB上B．在直线AB上C．在直线CB上D．都不对
18．函数y=lg（1-x）+lg（1+x）是（　　）
A．奇函数，且在（0，1）上是增函数B．奇函数，且在（0，1）上是减函数
C．偶函数，且在（0，1）上是增函数D．偶函数，且在（0，1）上是减函数
5．求圆心在直线x-3y=0上，与y轴相切，且被直线x-y=0截得的弦长为2$\sqrt{7}$的圆的方程．
15．（1班、3班做）已知函数f（x）=-$\frac{π}{12x}$，g（x）=xcosx-sinx，当x∈[-3π，3π]时，方程f（x）=g（x）的根的个数是（　　）
A．8B．6C．4D．2
2．为了得到函数y=sin（2x+$\frac{π}{3}$）的图象，只需将函数y=sinx的图象上所有的点（　　）
A．横坐标伸长到原来的2倍，再向左平行移动$\frac{π}{3}$个单位长度
B．横坐标缩短到原来的$\frac{1}{2}$倍，再向左平行移动$\frac{π}{3}$个单位长度
C．横坐标缩短到原来的$\frac{1}{2}$倍，再向左平行移动$\frac{π}{6}$个单位长度
D．横坐标缩短到原来的$\frac{1}{2}$倍，再向右平行移动$\frac{π}{6}$个单位长度
19．已知f（x）是一次函数，且满足3f（x+1）-f（x）=2x+9，g（x）是二次函数，且满足g（x）=0，g（x+1）=g（x）+x+1，则：
（1）求函数f（x）的解析式；
（2）求函数g（x）的解析式；
（3）画出h（x）=$\left\{\begin{array}{l}{f（x），x≥-2}\\{g（x），x＜-2}\end{array}\right.$的图象，并根据图象写出h（x）的最小值．
20．函数y=（$\frac{1}{2}$）|x|的图象大致为（　　）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网