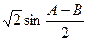题目内容
在△ABC中,已知a=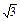 ,b=
,b=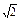 ,B=45°,求A、C和c.
,B=45°,求A、C和c.
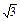 ,b=
,b=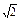 ,B=45°,求A、C和c.
,B=45°,求A、C和c.A=60°,C=75°,c=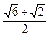 或A=120°,C=15°,c=
或A=120°,C=15°,c=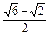 .
.
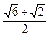 或A=120°,C=15°,c=
或A=120°,C=15°,c=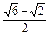 .
.∵B=45°<90°且asinB<b<a,∴△ABC有两解.
由正弦定理得sinA=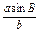 =
=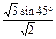 =
=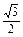 ,
,
则A为60°或120°.
①当A=60°时,C=180°-(A+B)=75°,
c=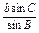 =
=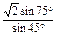 =
=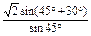 =
=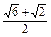 .
.
②当A=120°时,C=180°-(A+B)=15°,
c=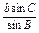 =
=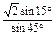 =
=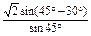 =
=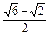 .
.
故在△ABC中,A=60°,C=75°,c=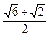 或
或
A=120°,C=15°,c=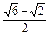 .
.
由正弦定理得sinA=
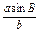 =
=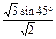 =
=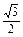 ,
,则A为60°或120°.
①当A=60°时,C=180°-(A+B)=75°,
c=
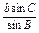 =
=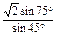 =
=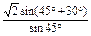 =
=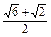 .
.②当A=120°时,C=180°-(A+B)=15°,
c=
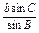 =
=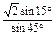 =
=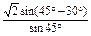 =
=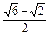 .
.故在△ABC中,A=60°,C=75°,c=
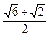 或
或A=120°,C=15°,c=
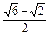 .
.
练习册系列答案
相关题目
 为钝角的
为钝角的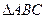 的内角A、B、C的对边分别为a、b、c,
的内角A、B、C的对边分别为a、b、c,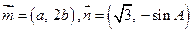 ,且
,且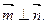 (1)求角
(1)求角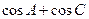 的取值范围.
的取值范围.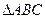 中,
中,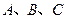 三内角所对的边分别为
三内角所对的边分别为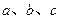 .
.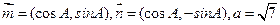 ,
,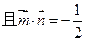
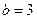 ,求
,求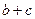 的最大值.
的最大值. 的周长为
的周长为 ,且
,且 .
. 的长.
的长. ,①求
,①求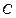 的正弦值. ②求
的正弦值. ②求 的值.
的值. 的方向,30 min后航行到B处,在B处看灯塔在船的北偏东
的方向,30 min后航行到B处,在B处看灯塔在船的北偏东 的方向,已知距离此灯塔6.5n mile以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?
的方向,已知距离此灯塔6.5n mile以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?

 中,若
中,若 ,
, ,则
,则 ( )
( )



 则三边的比
则三边的比 等于( )
等于( )