题目内容
7.已知{an}是公差不为零的等差数列,且a1=1,a2是a1与a5的等比中项.(1)求{an}的通项公式;
(2)求{an}的前n项和Sn.
分析 (1)根据等差数列的通项公式,利用等比中项列出方程,求出数列{an}的通项公式an;
(2)利用公式求出数列{an}的前n项和Sn.
解答 解:(1)等差数列{an}中,公差d≠0,且a1=1,
a2是a1与a5的等比中项,
∴${{a}_{2}}^{2}$=a1•a5,
即${{(a}_{1}+d)}^{2}$=a1(a1+4d),
∴(1+d)2=1+4d,
解得d=2或d=0(舍去);
∴数列{an}的通项公式为an=1+2(n-1)=2n-1;
(2)数列{an}的前n项和为
Sn=$\frac{{n(a}_{1}{+a}_{n})}{2}$=$\frac{n(1+2n-1)}{2}$=n2.
点评 本题考查了等差数列的通项公式与前n项和公式的应用问题,也考查了等比中项的应用问题,是基础题目.

练习册系列答案
相关题目
15.顶点在原点,且过点(-1,1)的抛物线的标准方程是( )
| A. | y2=-x | B. | x2=y | C. | y2=-x或x2=y | D. | y2=x或x2=-y |
19.圆C:(x+2)2+y2=32与抛物线y2=2px(p>0)相交于A、B两点,若直线AB恰好经过抛物线的焦点,则p等于( )
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 2 | D. | 4 |
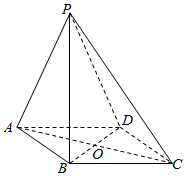 如图,四棱锥P-ABCD底面ABCD为平行四边形,且AC∩BD=O,PA=PC,PB⊥BD,平面PBD⊥平面PAC.
如图,四棱锥P-ABCD底面ABCD为平行四边形,且AC∩BD=O,PA=PC,PB⊥BD,平面PBD⊥平面PAC.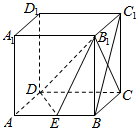 如图,在正方体ABCD-A1B1C1D1的棱长为a,若E为棱AB的中点,
如图,在正方体ABCD-A1B1C1D1的棱长为a,若E为棱AB的中点,