题目内容
12.已知点P的轨迹方程为(x+1)2+(y-2)2=1,直线l与点P的轨迹相切,且l在x轴. y轴上的截距相等,(1)若截距均为0,是否存在这样的直线,若存在,求直线l的方程.
(2)若截距不为0,是否存在这样的直线,若存在,求直线l的方程.
分析 (1)设P点坐标为(x,y),N点坐标为(x0,y0),则由中点坐标公式有$\left\{{\begin{array}{l}{x=\frac{{-2+{x_0}}}{2}}\\{y=\frac{{4+{y_0}}}{2}}\end{array}}\right.$$⇒\left\{{\begin{array}{l}{{x_0}=2x+2}\\{{y_0}=2y-4}\end{array}}\right.$,用未知点表示已知点,代入已知关系式中得到结论.
(2)因直线l在x轴、y轴上截距相等,故l的斜率存在且不为0,当直线l在x轴、y轴截距都为0时,设直线l的方程为:y=kx,并结合线圆相切得到斜率k的值,进而得到结论.
解答 解:(1)设P点坐标为(x,y),N点坐标为(x0,y0),
则由中点坐标公式有$\left\{{\begin{array}{l}{x=\frac{{-2+{x_0}}}{2}}\\{y=\frac{{4+{y_0}}}{2}}\end{array}}\right.$$⇒\left\{{\begin{array}{l}{{x_0}=2x+2}\\{{y_0}=2y-4}\end{array}}\right.$
∵N点在圆x2+y2=4上,
$\begin{array}{l}∴{x_0}^2+{y_0}^2=4\\∴{(2x+2)^2}+{(2y-4)^2}=4\\∴{(x+1)^2}+{(y-2)^2}=1\end{array}$
即为点P的轨迹方程…6分
(2)因直线l在x轴、y轴上截距相等,故l的斜率存在且不为0,
当直线l在x轴、y轴截距都为0时,设直线l的方程为:y=kx,即kx-y=0
∵直线l与(x+1)2+(y-2)2=1相切,∴$\frac{\left|-\right.k-\left.2\right|}{{\sqrt{{k^2}+1}}}=1⇒k=-\frac{3}{4}$…9分
当l在x轴、y轴上的截距均不为0时,设直线l的方程为$:\frac{x}{a}+\frac{y}{a}=1$,即x+y-a=0
∵直线l与(x+1)2+(y-2)2=1相切,∴$\frac{{|{-1+2-a}|}}{{\sqrt{2}}}=1⇒a=1±\sqrt{2}$,
故直线l的方程为$x+y-1-\sqrt{2}=0$或$x+y-1+\sqrt{2}=0$
综上可知l的方程为:$y=-\frac{3}{4}x$
或$x+y-1-\sqrt{2}=0$或$x+y-1+\sqrt{2}=0$…12分
点评 本试题主要是考查了利用相关点法求解轨迹方程,以及利用直线与圆相切,确定参数的值,并利用直线在两坐标轴上截距相等得到直线的方程.

| A. | ¬p或q | B. | p且q | C. | p或q | D. | ¬p且¬q |
| A. | m=3 | B. | m=0 | C. | m=0或m=3 | D. | m=0或m=-1 |
 在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是棱AB和BC上的动点,且AE=BF.
在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是棱AB和BC上的动点,且AE=BF.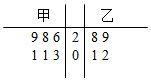 为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论:
为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.考虑以下结论: