题目内容
2.${∫}_{-3}^{-1}$$\sqrt{1-(x+2)^{2}}$dx=$\frac{π}{2}$.分析 作出函数图象,根据定积分的几何意义求出函数与x轴所围成区域的面积.
解答 解:令y=$\sqrt{1-(x+2)^{2}}$,则(x+2)2+y2=1.
∴y=$\sqrt{1-(x+2)^{2}}$(-3≤x≤-1)表示以(-2,0)为圆心,以1为半径的半圆.
∴${∫}_{-3}^{-1}$$\sqrt{1-(x+2)^{2}}$dx=$\frac{1}{2}×π×{1}^{2}$=$\frac{π}{2}$.
故答案为:$\frac{π}{2}$.
点评 本题考查了定积分的几何意义,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.执行如图的程序框图,如果输入的N=100,则输出的x=( )
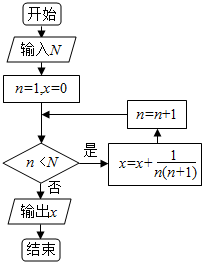

| A. | 0.95 | B. | 0.98 | C. | 0.99 | D. | 1.00 |
10.设α,β∈[0,π],且满足sinαcosβ-cosαsinβ=1,则sin(2α-β)+sin(α-2β)的取值范围为( )
| A. | [-$\sqrt{2}$,1] | B. | [-1,$\sqrt{2}$] | C. | [-1,1] | D. | [1,$\sqrt{2}$] |