题目内容
1.已知点A的坐标为(-1,0),点B是圆心为C的圆(x-1)2+y2=16上一动点,线段AB的垂直平分线交BC与点M,则动点M的轨迹方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.分析 利用椭圆的定义判断点M的轨迹是以A、C为焦点的椭圆,求出a、b的值,即得椭圆的方程.
解答 解:由题意得,圆心C(1,0),半径等于4,
连接MA,则|MA|=|MB|,
∴|MC|+|MA|=|MC|+|MB|=|BC|=4>|AC|=2,
故点M的轨迹是:以A、C为焦点的椭圆,2a=4,即有a=2,c=1,
∴b=$\sqrt{3}$,
∴椭圆的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
故答案为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
点评 本题考查用定义法求点的轨迹方程,考查学生转化问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
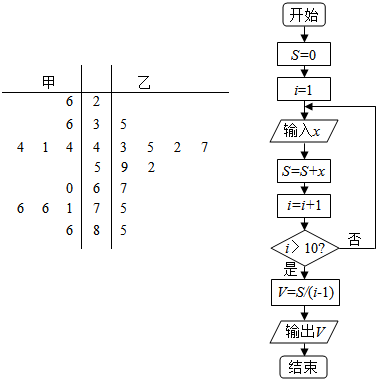 为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.
为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.