题目内容
在△ABC中，a、b、c分别表示三个内角∠A、∠B、∠C的对边，如果(a2＋b2)sin(A－B)＝(a2－b2)sin(A＋B)，判断三角形的形状．
解：已知等式可化为a2[sin(A－B)－sin(A＋B)]＝
b2[－sin(A＋B)－sin(A－B)]，
∴ 2a2cosAsinB＝2b2cosBsinA.
由正弦定理得sin2AcosAsinB＝sin2BcosBsinA，
∴ sinAsinB(sinAcosA－sinBcosB)＝0，∴ sin2A＝sin2B.由0<2A<2π，0<2B<2π得2A＝2B或2A＝π－2B，即△ABC为等腰或直角三角形．
练习册系列答案
相关题目
在如图的表格中，每格填上一个数字后，使每一横行成等差数列，每一纵列成等比数列，则a＋b＋c＝________．
| 1 | 2 | |||
| 0.5 | 1 | |||
| a | ||||
| b | ||||
| c |
，
，
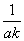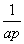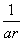成等差数列？若存在，用k分别表示p和r(只要写出一组)；若不存在，请说明理由．
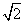，b＝2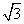
，cosC＝
，则△ABC的面积为________．
，C＝
，则△ABC的面积为________．
)海里的两个观测点，现位于A点北偏东45°、B点北偏西60°的D点有一艘轮船发出求救信号，位于B点南偏西60°且与B点相距20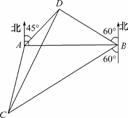
，且
，则cos2θ＝________．