题目内容
马老师从课本上抄录一个随机变量ξ的概率分布律如下表:
| x | 1 | 2 | 3 |
| P(ξ=x) | ? | ! | ? |
2
分析:根据已知设出P(ξ=1)=P(ξ=3)=a,P(ξ=2)=b,且根据离散型随机变量分布列的性质知2a+b=1,根据离散型随机变量分布列的期望求法即可求得结果.在计算过程中注意整体性.
解答:设P(ξ=1)=P(ξ=3)=a,P(ξ=2)=b,
则2a+b=1,
Eξ=a+2b+3a=2(2a+b)=2,
故答案为2.
点评:此题是个基础题.考查离散型随机变量的期望和方差,在计算过程中注意离散型随机变量分布列的性质和整体代换.
分析:根据已知设出P(ξ=1)=P(ξ=3)=a,P(ξ=2)=b,且根据离散型随机变量分布列的性质知2a+b=1,根据离散型随机变量分布列的期望求法即可求得结果.在计算过程中注意整体性.
解答:设P(ξ=1)=P(ξ=3)=a,P(ξ=2)=b,
则2a+b=1,
Eξ=a+2b+3a=2(2a+b)=2,
故答案为2.
点评:此题是个基础题.考查离散型随机变量的期望和方差,在计算过程中注意离散型随机变量分布列的性质和整体代换.

练习册系列答案
相关题目
 ,其中a、b∈R,g(x)=ex(e是自然对数的底).
,其中a、b∈R,g(x)=ex(e是自然对数的底). ;
;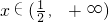 恒成立,求a的取值范围.
恒成立,求a的取值范围. ,若|m+1|*|m|=|m+1|,则实数m的取值范围是
,若|m+1|*|m|=|m+1|,则实数m的取值范围是 )
) 将图中的正方体标上字母,使其成为正方体ABCD-A1B1C1D1,不同的标字母方式共有
将图中的正方体标上字母,使其成为正方体ABCD-A1B1C1D1,不同的标字母方式共有

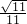
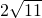
 ,c=2,那么B等于
,c=2,那么B等于