题目内容
5.如果f(x)=ax2+bx+c,f(x)>0的解集为{x|x<-2或x>4},那么( )| A. | f(5)<f(2)<f(-1) | B. | f(2)<f(5)<f(-1) | C. | f(-1)<f(2)<f(5) | D. | f(2)<f(-1)<f(5) |
分析 根据函数f(x)>0的解集得到函数f(x)的对称轴和开口方向,从而比较出函数值的大小即可.
解答 解:f(x)=ax2+bx+c,
f(x)>0的解集为{x|x<-2或x>4},
故函数f(x)的对称轴是x=1,开口向上,
由2-1<1-(-1)<5-1,
故得:f(2)<f(-1)<f(5),
故选:D.
点评 本题考查了二次函数的性质,考查函数值的大小比较,是一道基础题.

练习册系列答案
相关题目
15.一离散型随机变量X的概率分布列为
且E(X)=1.5,则a-b=0.
| X | 0 | 1 | 2 | 3 |
| P | 0.1 | a | b | 0.1 |
13.在△ABC中,内角A、B、C所对的边分别为a、b、c,若$sin({\frac{3}{2}B+\frac{π}{4}})=\frac{{\sqrt{2}}}{2}$,且a+c=2,则△ABC周长的取值范围是( )
| A. | (2,3] | B. | [3,4) | C. | (4,5] | D. | [5,6) |
14.关于x的方程$({m+1}){x^{{m^2}+1}}+4x+2=0$是一元二次方程,则m的值为( )
| A. | m1=-1,m2=1 | B. | m=1 | C. | m=-1 | D. | 无解 |
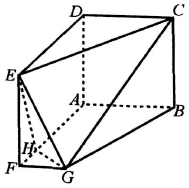 在多面体ABCDEFG中,四边形ABCD与ADEF是边长均为a的正方形,四边形ABGH是直角梯形,AB⊥AF,且FA=2FG=4FH.
在多面体ABCDEFG中,四边形ABCD与ADEF是边长均为a的正方形,四边形ABGH是直角梯形,AB⊥AF,且FA=2FG=4FH. 如图所示是一次歌咏大赛上,七位评委为某选手打出的分数的茎叶图,则中位数是86.
如图所示是一次歌咏大赛上,七位评委为某选手打出的分数的茎叶图,则中位数是86.