题目内容
10.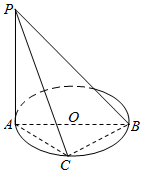 如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面ABC
如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面ABC(I)证明:平面PAC丄平面PBC;
(Ⅱ)设PA=$\sqrt{3}$,AC=1,求三棱锥A-PBC的高.
分析 (1)由直径性质得BC⊥AC,由线面垂直得PA⊥BC,由此能证明平面PAC⊥平面PBC.
(2)过点A作PC的垂线,垂足为D,由已知得AD为三棱锥A-PBC的高,由此能求出结果.
解答 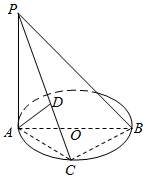 证明:(1)∵AB是⊙O的直径,点C是⊙O上的动点
证明:(1)∵AB是⊙O的直径,点C是⊙O上的动点
∴∠ACB=90°,即BC⊥AC,
又∵PA⊥⊙O所在平面,BC?平面⊙O,
∴PA⊥BC,∴PA∩AC=A,
∴BC⊥平面PCB,∴平面PAC⊥平面PBC.
解:(2)由(1)的结论平面PAC⊥平面PBC,平面PAC∩平面PBC=PC,
∴过点A作PC的垂线,垂足为D,则AD为三棱锥A-PBC的高,
在Rt△PAC中,PA=$\sqrt{3}$,AC=1,∴PC=2,
由AD×PC=PA×AC,得AD=$\frac{PA×AC}{PC}=\frac{1×\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$.
∴三棱锥A-PBC的高为$\frac{\sqrt{3}}{2}$.
点评 本题考查面面垂直的证明,考查三棱锥的高的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
15.在正方体ABCD-A1B1C1D1中,P为对角线BD1上靠近B的三等分点,P到各顶点的距离的不同取值有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
2.将3个半径为1的球和一个半径为$\sqrt{2}-1$的球叠为两层放在桌面上,上层只放一个较小的球,四个球两两相切,那么上层小球的最高点到桌面的距离是( )
| A. | $\frac{{3\sqrt{2}+\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{3}+2\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{2}+2\sqrt{6}}}{3}$ | D. | $\frac{{2\sqrt{2}+\sqrt{6}}}{3}$ |
20.定义2×2矩阵$|\begin{array}{l}{{a}_{1}}&{{a}_{2}}\\{{a}_{3}}&{{a}_{4}}\end{array}|$=a1a4-a2a3,若f(x)=$|\begin{array}{l}{co{s}^{2}x-si{n}^{2}x}&{\sqrt{3}}\\{cos(\frac{π}{2}+2x)}&{1}\end{array}|$,则f(x)的图象向右平移$\frac{π}{3}$个单位得到函数g(x),则函数g(x)的解析式为( )
| A. | 图象关于(π,0)中心对称 | B. | 图象关于直线x=$\frac{π}{2}$对称 | ||
| C. | g(x)是周期为π的奇函数 | D. | 在区间[-$\frac{π}{6}$,0]上单调递增 |
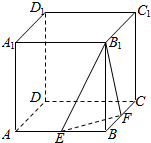 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是棱AB和BC的中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是棱AB和BC的中点.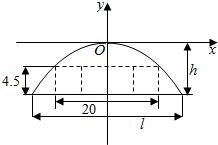 某隧道设计为双向四车道,车道总宽20米,要求通行车辆限高4.5米,隧道口截面的拱线近似地看成抛物线形状的一部分,如图所示建立平面直角坐标系xOy.
某隧道设计为双向四车道,车道总宽20米,要求通行车辆限高4.5米,隧道口截面的拱线近似地看成抛物线形状的一部分,如图所示建立平面直角坐标系xOy.