题目内容
15.在正方体ABCD-A1B1C1D1中,P为对角线BD1上靠近B的三等分点,P到各顶点的距离的不同取值有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
分析 取底面ABCD的中心O,连接PA,PC,PO,由P是BD1的三等分点,推导出PB≠PD1≠PB1≠PD,从而得到点P到正方体的顶点的不同距离有4个.
解答 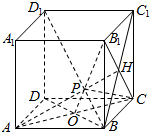 解:如图,取底面ABCD的中心O,连接PA,PC,PO.∵AC⊥平面DD1B,
解:如图,取底面ABCD的中心O,连接PA,PC,PO.∵AC⊥平面DD1B,
又PO?平面DD1B,∴AC⊥PO.
又O是AC的中点,∴PA=PC.
同理,取B1C与BC1的交点H,则B1C⊥平面D1C1B,
∴B1C⊥PH.又H是B1C的中点,∴PB1=PC,
∴PA=PB1=PC.
同理可证PA1=PC1=PD.
又P是BD1的三等分点,
∴PB≠PD1≠PB1≠PD,
故点P到正方体的顶点的不同距离有4个.
故选:B.
点评 本题题考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
4.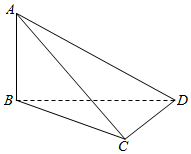 如图,在四面体ABCD中,AB⊥BD,CD⊥DB,若AB与CD所成的角的大小为60°,则二面角C-BD-A的大小为( )
如图,在四面体ABCD中,AB⊥BD,CD⊥DB,若AB与CD所成的角的大小为60°,则二面角C-BD-A的大小为( )
 如图,在四面体ABCD中,AB⊥BD,CD⊥DB,若AB与CD所成的角的大小为60°,则二面角C-BD-A的大小为( )
如图,在四面体ABCD中,AB⊥BD,CD⊥DB,若AB与CD所成的角的大小为60°,则二面角C-BD-A的大小为( )| A. | 60°或90° | B. | 60° | C. | 60°或120° | D. | 30°或150° |
 如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠ABC=60°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PO=$\sqrt{6}$.
如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠ABC=60°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PO=$\sqrt{6}$.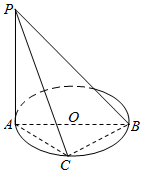 如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面ABC
如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面ABC
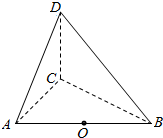 如图所示,三棱锥D-ABC中,AC,BC,CD两两垂直,AC=CD=1,$BC=\sqrt{3}$,点O为AB中点.
如图所示,三棱锥D-ABC中,AC,BC,CD两两垂直,AC=CD=1,$BC=\sqrt{3}$,点O为AB中点.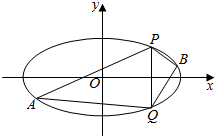 已知中心在原点,焦点在x轴上的椭圆C的离心率为$\frac{\sqrt{3}}{2}$,点(0,$\sqrt{2}$)是椭圆与y轴的一个交点.
已知中心在原点,焦点在x轴上的椭圆C的离心率为$\frac{\sqrt{3}}{2}$,点(0,$\sqrt{2}$)是椭圆与y轴的一个交点.