题目内容
17.已知在关于x的不等式loga(x2-4)>loga(6x-13a)(0<a<1)的解集中,有且只有两个整数解,则实数a的取值范围是[$\frac{9}{13}$,$\frac{12}{13}$).分析 根据对数函数的单调性,将不等式进行转化求解即可.
解答 解:∵0<a<1,
∴由loga(x2-4)>loga(6x-13a)得$\left\{\begin{array}{l}{{x}^{2}-4>0}\\{6x-13a>0}\\{{x}^{2}-4<6x-13a}\end{array}\right.$.
即$\left\{\begin{array}{l}{x>2或x<-2}\\{x>\frac{13a}{6}}\\{{x}^{2}-6x-4<-13a}\end{array}\right.$,
即$\left\{\begin{array}{l}{x>2}\\{x>\frac{13a}{6}}\\{3-\sqrt{13-13a}<x<3+\sqrt{13-13a}}\end{array}\right.$,
要使不等式组有且只有两个整数解,
则这两个整数只能是3和4,
则4<3+$\sqrt{13-13a}$≤5,
即1<$\sqrt{13-13a}$≤2,
平方得1<13-13a≤4,
得$\frac{9}{13}$≤a<$\frac{12}{13}$,
即实数a的取值范围是[$\frac{9}{13}$,$\frac{12}{13}$),
故答案为:[$\frac{9}{13}$,$\frac{12}{13}$)
点评 本题主要考查对数不等式的求解,根据对数函数的单调性进行转化是解决本题的关键.考查学生的运算和转化能力.

练习册系列答案
相关题目
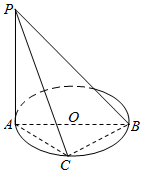 如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面ABC
如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面ABC