题目内容
5.函数f(x)=lnx+x2-bx+a(b>0,a∈R)的图象在点(b,f(b))处的切线斜率的最小值是( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1 | D. | 2 |
分析 求出原函数的导函数,得到函数在x=b时的导数值,利用基本不等式求最值得答案.
解答 解:由f(x)=lnx+x2-bx+a,得f′(x)=$\frac{1}{x}$+2x-b(x>0),
∴f′(b)=$\frac{1}{b}$+b(b>0)
∴f′(b)=$\frac{1}{b}$+b≥2,
当且仅当b=$\frac{1}{b}$,即b=1时上式取“=”,切线斜率的最小值是2.
故选:D.
点评 本题考查了利用导数研究过曲线上某点处的切线方程,考查了利用基本不等式求最值,是基础题.

练习册系列答案
相关题目
14.已知集合A={x∈Z|-1≤x≤2},B={x|log3x<1},则A∩B=( )
| A. | {-1,0,1,2} | B. | {0,1,2} | C. | {0,1} | D. | {1,2} |
15.下列结论中正确的是( )
| A. | ∵a∥α,b∥α,∴a∥b | B. | ∵a∥α,b?α,∴a∥b | C. | ∵α∥β,a∥β,∴a∥α | D. | ∵α∥β,a?β,∴a∥α |
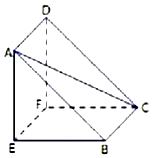 如图所示为一名曰“堑堵”的几何体,已知AE⊥底面BCFE,DF∥AE,DF=AE=1,CE=$\sqrt{7}$,四边形ABCD是正方形.
如图所示为一名曰“堑堵”的几何体,已知AE⊥底面BCFE,DF∥AE,DF=AE=1,CE=$\sqrt{7}$,四边形ABCD是正方形. 如图,在四棱锥P-ABCD中,底面ABCD是长方形,侧棱PD⊥底面ABCD,且PD=AD=1,DC=2,过D作DF⊥PB于F,过F作FE⊥PB交PC于E.
如图,在四棱锥P-ABCD中,底面ABCD是长方形,侧棱PD⊥底面ABCD,且PD=AD=1,DC=2,过D作DF⊥PB于F,过F作FE⊥PB交PC于E.