题目内容
17.已知函数f(x)是定义在R上的奇函数,若g(x)=f(x+1)+5,g′(x)为g(x)的导函数,对?x∈R,总有g′(x)>2x,则g(x)<x2+4的解集为(-∞,-1).分析 求出g(x)的图象关于点(-1,5)对称,令h(x)=g(x)-x2-4,根据函数的单调性求出不等式的解集即可.
解答 解:因为函数f(x)是定义在R上的奇函数,
所以函数f(x)关于原点对称,
又g(x)=f(x+1)+5,
故g(x)的图象关于点(-1,5)对称,
令h(x)=g(x)-x2-4,
∴h′(x)=g′(x)-2x,
∵对?x∈R,g′(x)>2x,
∴h(x)在R上是增函数,
又h(-1)=g(-1)-(-1)2-4=0,
∴g(x)<x2+4的解集是(-∞,-1),
故答案为:(-∞,-1).
点评 本题考查了解不等式问题,考查函数的单调性以及导数的应用,考查对称性,是一道中档题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
5.函数f(x)=lnx+x2-bx+a(b>0,a∈R)的图象在点(b,f(b))处的切线斜率的最小值是( )
| A. | 2$\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1 | D. | 2 |
6.已知实数x,y满足约束条件$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-5≥0\\ y-2≤0\end{array}\right.$,函数f(x)=logc(x+2)-1(c>0,c≠1)的图象恒过定点A(a,b),则$z=\frac{y-b}{x-a}$的取值范围是( )
| A. | $[\frac{1}{3},2]$ | B. | $[\frac{2}{5},1]$ | C. | $[\frac{1}{2},\frac{3}{2}]$ | D. | $[\frac{3}{2},\frac{5}{2}]$ |
 如图长方体ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别为CB1、CD1、AB的中点.
如图长方体ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别为CB1、CD1、AB的中点.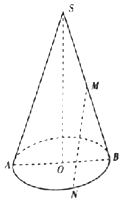 如图,平面SAB为圆锥的轴截面,O为底面圆的圆心,M为母线SB的中点,N为底面圆周上的一点,AB=4,SO=6.
如图,平面SAB为圆锥的轴截面,O为底面圆的圆心,M为母线SB的中点,N为底面圆周上的一点,AB=4,SO=6.