题目内容
9．已知等差数列{an}的第8项是二项式（x+$\frac{1}{x}$+y）4展开式的常数项，则a9-$\frac{1}{3}$a11=（ ）| A． | $\frac{2}{3}$ | B． | 2 | C． | 4 | D． | 6 |
分析 由二项式系数的性质求出二项式（x+$\frac{1}{x}$+y）4展开式的常数项，得到a8=6，由等差数列的通项公式把a9-$\frac{1}{3}$a11转化为$\frac{2}{3}{a}_{8}$得答案．
解答 解：∵（x+$\frac{1}{x}$+y）4的展开式中的常数项为${C}_{4}^{0}•{C}_{4}^{2}{x}^{2}（\frac{1}{x}）^{2}{y}^{0}=6$，
∴a8=6，
又数列{an}为等差数列，
∴a9-$\frac{1}{3}$a11=${a}_{1}+8d-\frac{1}{3}（{a}_{1}+10d）$=$\frac{2}{3}（{a}_{1}+7d）=\frac{2}{3}{a}_{8}=\frac{2}{3}×6=4$．
故选：C．
点评 本题考查二项式系数的性质，考查了等差数列的通项公式，是基础的计算题．
练习册系列答案
相关题目
的左、右焦点分别为
，离心率为
，经过点
且倾斜角为
的直线
交椭圆于
两点．
的周长为16，求直线
的方程；
，求椭圆
的方程．
的定义域，值域分别是
、
，则
（ ）
B．
C．
D．
17．
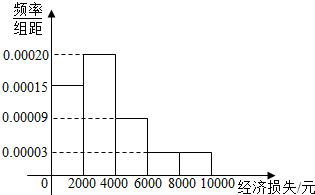2015年7月9日21时15分，台风“莲花”在我国广东省陆丰市甲东镇沿海登陆，给当地人民造成了巨大的财产损失，适逢暑假，小张调查了当地某小区的100户居民由于台风造成的经济损失，将收集的数据分成[0，2000]，（2000，4000]，（4000，6000]，（6000，8000]，（8000，10000]五组，并作出如下频率分布直方图（图1）：
（1）台风后居委会号召小区居民为台风重灾区捐款，小张调查的100户居民捐款情况如右下表格，在图2表格空白处填写正确数字，并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关？
（2）将上述调查所得到的频率视为概率．现在从该地区大量受灾居民中，采用随机抽样方法每次抽取1户居民，抽取3次，记被抽取的3户居民中自身经济损失超过4000元的人数为ξ．若每次抽取的结果是相互独立的，求ξ的分布列，期望E（ξ）和方差D（ξ）．
附：临界值表
随机量变${K^2}=\frac{{（a+b+c+d）{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．
2015年7月9日21时15分，台风“莲花”在我国广东省陆丰市甲东镇沿海登陆，给当地人民造成了巨大的财产损失，适逢暑假，小张调查了当地某小区的100户居民由于台风造成的经济损失，将收集的数据分成[0，2000]，（2000，4000]，（4000，6000]，（6000，8000]，（8000，10000]五组，并作出如下频率分布直方图（图1）：（1）台风后居委会号召小区居民为台风重灾区捐款，小张调查的100户居民捐款情况如右下表格，在图2表格空白处填写正确数字，并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关？
（2）将上述调查所得到的频率视为概率．现在从该地区大量受灾居民中，采用随机抽样方法每次抽取1户居民，抽取3次，记被抽取的3户居民中自身经济损失超过4000元的人数为ξ．若每次抽取的结果是相互独立的，求ξ的分布列，期望E（ξ）和方差D（ξ）．
| 经济损失不超过 4000元 | 经济损失超过 4000元 | 合计 | |
| 捐款超过 500元 | 60 | ||
| 捐款不超 过500元 | 10 | ||
| 合计 |
| P（K2≥k） | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
14．直线x+1=0的倾斜角为（ ）
| A． | 90° | B． | 45° | C． | 135° | D． | 60° |
18．下列求导正确的是（ ）
| A． | （$\frac{1}{x}$）′=$\frac{1}{{x}^{2}}$ | B． | （log2x）′=$\frac{1}{xln2}$ | C． | （3x+1）′=x•3x-1+1 | D． | （cosx）′=sinx |