��Ŀ����
17��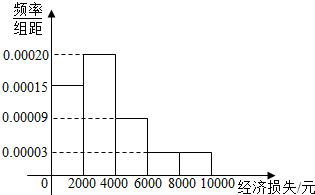 2015��7��9��21ʱ15�֣�̨�硰���������ҹ��㶫ʡ½���м����غ���½����������������˾�IJƲ���ʧ���ʷ���٣�С�ŵ����˵���ijС����100����������̨����ɵľ�����ʧ�����ռ������ݷֳ�[0��2000]����2000��4000]����4000��6000]����6000��8000]����8000��10000]���飬����������Ƶ�ʷֲ�ֱ��ͼ��ͼ1����
2015��7��9��21ʱ15�֣�̨�硰���������ҹ��㶫ʡ½���м����غ���½����������������˾�IJƲ���ʧ���ʷ���٣�С�ŵ����˵���ijС����100����������̨����ɵľ�����ʧ�����ռ������ݷֳ�[0��2000]����2000��4000]����4000��6000]����6000��8000]����8000��10000]���飬����������Ƶ�ʷֲ�ֱ��ͼ��ͼ1������1��̨����ί�����С������Ϊ̨����������С�ŵ����100����������������±�����ͼ2����հ״���д��ȷ���֣���˵���Ƿ���95%���ϵİ�����Ϊ���������ڻ�����500Ԫ������������ʧ�Ƿ�4000Ԫ�йأ�
��2���������������õ���Ƶ����Ϊ���ʣ����ڴӸõ����������־����У����������������ÿ�γ�ȡ1������ȡ3�Σ��DZ���ȡ��3������������������ʧ����4000Ԫ������Ϊ�Σ���ÿ�γ�ȡ�Ľ����������ģ���εķֲ��У�����E���Σ��ͷ���D���Σ���
| ������ʧ������ 4000Ԫ | ������ʧ���� 4000Ԫ | �ϼ� | |
| ���� 500Ԫ | 60 | ||
| ���� ��500Ԫ | 10 | ||
| �ϼ� |
| P��K2��k�� | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
���� ��1����Ƶ�ʷֲ�ֱ��ͼ��֪���ڳ�ȡ��100���У�������ʧ������4000Ԫ����70�ˣ�������ʧ����4000Ԫ����30�ˣ����K2���õ���95%���ϵİ�����Ϊ��������Ƿ���ڻ�����500Ԫ������������ʧ�Ƿ�4000Ԫ�йأ�
��2����Ƶ�ʷֲ�ֱ��ͼ��֪�鵽����������ʧ����4000Ԫ�����Ƶ��Ϊ0.3����Ƶ����Ϊ���ʣ�������֪�ε�ȡֵ������0��1��2��3���ҦΡ�B��3��$\frac{3}{10}$�����ɴ�������εķֲ��У�����E���Σ��ͷ���D���Σ���
��� ����С������12�֣�
�⣺��1����Ƶ�ʷֲ�ֱ��ͼ��֪���ڳ�ȡ��100���У�������ʧ������4000Ԫ����70�ˣ�
������ʧ����4000Ԫ����30�ˣ�������������£�
| ������ʧ������ 4000Ԫ | ������ʧ���� 4000Ԫ | �ϼ� | |
| ���� 500Ԫ | 60 | 20 | 80 |
| ���� ��500Ԫ | 10 | 10 | 20 |
| �ϼ� | 70 | 30 | 100 |
K2=$\frac{100����60��10-10��20��^{2}}{80��20��70��30}$=4.76
��4.762��3.841��p��k��3.841��=0.05
����95%���ϵİ�����Ϊ��������Ƿ���ڻ�����500Ԫ������������ʧ�Ƿ�4000Ԫ�йأ�����4�֣�
��2����Ƶ�ʷֲ�ֱ��ͼ��֪�鵽����������ʧ����4000Ԫ�����Ƶ��Ϊ0.3����Ƶ����Ϊ���ʣ�
������֪�ε�ȡֵ������0��1��2��3���ҦΡ�B��3��$\frac{3}{10}$��������5�֣�
$p����=0��=C_3^0{��\frac{3}{10}��^0}��{��\frac{7}{10}��^3}=\frac{343}{1000}$������6�֣�
$p����=1��=C_3^1{��\frac{3}{10}��^1}��{��\frac{7}{10}��^2}=\frac{441}{1000}$������7�֣�
$p����=2��=C_3^2{��\frac{3}{10}��^2}��{��\frac{7}{10}��^1}=\frac{189}{1000}$������8�֣�
$p����=3��=C_3^3{��\frac{3}{10}��^3}��{��\frac{7}{10}��^0}=\frac{27}{1000}$������9�֣�
��εķֲ���Ϊ��
| �� | 0 | 1 | 2 | 3 |
| p | $\frac{343}{1000}$ | $\frac{441}{1000}$ | $\frac{189}{1000}$ | $\frac{27}{1000}$ |
$E���Σ�=np=3��\frac{3}{10}=0.9$������11�֣�
$D���Σ�=np��1-p��=3��\frac{3}{10}��\frac{7}{10}=0.63$����12�֣�
���� ���⿼����ɢ����������ķֲ��У������ͷ���������е��⣬����ʱҪ�������⣬ע�����ֲ������ʵĺ������ã�

��ϰ��ϵ�д�
�����Ŀ
5����֪˫����$\frac{x^2}{9}-\frac{y^2}{4}=1$�����˫���ߵĽ����߷���Ϊ��������
| A�� | 9x��4y=0 | B�� | 4x��9y=0 | C�� | 3x��2y=0 | D�� | 2x��3y=0 |
2����M�ǡ�ABC����ƽ����һ�㣬$\overrightarrow{AC}+\overrightarrow{AB}=2\overrightarrow{AM}$������
| A�� | $\overrightarrow{MC}+\overrightarrow{MB}=\overrightarrow 0$ | B�� | $\overrightarrow{MC}+\overrightarrow{AB}=\overrightarrow 0$ | C�� | $\overrightarrow{AM}+\overrightarrow{BC}=\overrightarrow 0$ | D�� | $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow 0$ |
9����֪�Ȳ�����{an}�ĵ�8���Ƕ���ʽ��x+$\frac{1}{x}$+y��4չ��ʽ�ij������a9-$\frac{1}{3}$a11=��������
| A�� | $\frac{2}{3}$ | B�� | 2 | C�� | 4 | D�� | 6 |
7��sin750���ֵ�ǣ�������
| A�� | $\frac{1}{2}$ | B�� | -$\frac{1}{2}$ | C�� | $\frac{\sqrt{3}}{2}$ | D�� | -$\frac{\sqrt{3}}{2}$ |
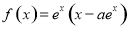 ������
������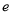 Ϊ��Ȼ�����ĵ�����ǡ��������ֵ��
Ϊ��Ȼ�����ĵ�����ǡ��������ֵ��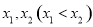 ��������˵������ȷ���ǣ� ��
��������˵������ȷ���ǣ� ��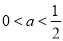 B��
B��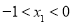
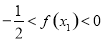 D��
D��
 ������
������ �ϵ����ݼ�����
�ϵ����ݼ����� �ϵ�����������ʵ��
�ϵ�����������ʵ�� ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��