��Ŀ����
4����������Ǧ��ͦ£��������+��=$\frac{��}{2}$����Ʀ��ͦ¡����廥�ࡱ����֪sin����+�ȣ�=-$\frac{1}{3}$����sin��=$\frac{2\sqrt{2}}{3}$����cos����+�ã�=$\frac{1}{3}$����tan��=-2$\sqrt{2}$����tan��=$\frac{\sqrt{2}}{4}$�����Ǧ��У�������Ǧȡ����廥�ࡱ���ǣ�������
| A�� | �٢� | B�� | �ڢ� | C�� | �٢� | D�� | �ڢ� |
���� ������֪�ɵ�sin2��+sin2����+�ȣ�=1���ã�$\frac{��}{2}$+��+��+2k��=0�����+��+2k��=$\frac{��}{2}$��k��Z���������жϦȺͦÿ����ǹ��廥�ࣻ
������sin��=sin����-$\frac{��}{2}$������æ�-��=2k��-$\frac{��}{2}$�����+��=2k��+$\frac{3��}{2}$�����ɵý�Ⱥͦò������ǹ��廥�ࣻ
�۽�á�sin��=sin��$\frac{��}{2}$-�ã�����sin��=sin��$\frac{��}{2}$-�ã�ʱ���ɵæ�=$\frac{��}{2}$-��+2k�У���k��Z�����ɵ�a�ͦ��п����ǹ��廥�ࣻ
�ܽ��cos2��+sin2��=1���ɵæ�-��=2k�У��ɵæúͦȲ������ǹ��廥�࣮
��� �⣺��sin����+�ȣ�=-$\frac{1}{3}$���ɵã�sin��=$\frac{1}{3}$��
���sin2��+sin2����+�ȣ�=1���ɵã�$\frac{��}{2}$+��+��+2k��=0�����+��+2k��=$\frac{��}{2}$��k��Z�����ʦȺͦÿ����ǹ��廥�ࣻ
��cos����+�ã�=-cos��=-sin����+�ȣ�=sin��=sin����-$\frac{��}{2}$����
���=��-$\frac{��}{2}$+2k�����=��-����-$\frac{��}{2}$��+2k����k��Z����
���-��=2k��-$\frac{��}{2}$�����+��=2k��+$\frac{3��}{2}$����k��Z����
��+�²����ܵ���90�㣬�Ⱥͦò������ǹ��廥�ࣻ
�۵�tan��=-2$\sqrt{2}$ʱ���ɵ�cos��=��$\frac{1}{3}$=��sin��=sin��$\frac{��}{2}$-�ã���
��sin��=sin��$\frac{��}{2}$-�ã�ʱ���ɵæ�=$\frac{��}{2}$-��+2k�У���k��Z����
�ɵ�a�ͦ��п����ǹ��廥�ࣻ
�ܵ�tan��=$\frac{\sqrt{2}}{4}$ʱ��cos��=��$\frac{2\sqrt{2}}{3}$����ʱcos2��+sin2��=1����-��=2k�У���k��Z����
��úͦȲ������ǹ��廥�࣮
��ѡ��C��
���� ������Ҫ���������Ǻ����յ���ʽ�����ã����������Ǻ�����ͼ������ʣ�������ѧ�������ͽ������������������е��⣮

 ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�| A�� | $\frac{2}{3}$ | B�� | 2 | C�� | 4 | D�� | 6 |
 ����
����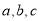 �Ĵ�С��ϵΪ�� ��
�Ĵ�С��ϵΪ�� ��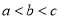 B��
B��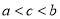
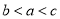 D��
D��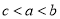
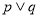 Ϊ�����⣬��
Ϊ�����⣬��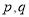 ��Ϊ�����⣻
��Ϊ�����⣻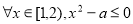 ��Ϊ�������һ����ֲ���Ҫ����������
��Ϊ�������һ����ֲ���Ҫ����������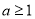 ��
��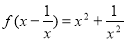 ����
����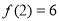 ��
��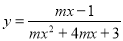 �Ķ�����Ϊ
�Ķ�����Ϊ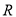 ����ʵ��
����ʵ��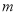 ��ȡֵ��Χ��
��ȡֵ��Χ��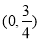 ��
��