题目内容
已知等差数列{an}的公差d≠0,若a5、a9、a15成等比数列,那么公比为( )
A. | B. | C. | D. |
C
试题分析:先利用等差数列的通项公式,用a1和d分别表示出等差数列的第5、9、15项进而利用等比中项的性质建立等式求得a1和d的关系,进而利用q=
 求得答案. 解:依题意可知(a1+8d)2=(a1+4d)(a1+14d),整理得2a1d=8d2,解得4d=a1,∴q=
求得答案. 解:依题意可知(a1+8d)2=(a1+4d)(a1+14d),整理得2a1d=8d2,解得4d=a1,∴q= =
= =
= ;故选C.
;故选C.点评:本题主要考查了等比数列的性质和等差数列的通项公式.属基础题.

练习册系列答案
相关题目
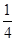 an bn,求数列{cn}的前n项和Tn.
an bn,求数列{cn}的前n项和Tn.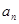 }的前n项和为
}的前n项和为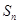 ,
,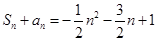 ,
,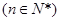 .
.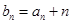 ,证明:数列
,证明:数列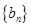 是等比数列;
是等比数列;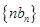 的前
的前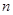 项和
项和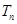 ;
; ,
, ,
, ,记
,记
 ,
,
 ,
,
 (
( ),若对于任意
),若对于任意 ,
, ,
, 成等差数列.
成等差数列. 的前
的前 项和.
项和. 是等差数列,其前
是等差数列,其前 项和为
项和为 ;
; 是等比数列,且
是等比数列,且 .
.  的前
的前 .
. }为等差数列,公差d = -2,
}为等差数列,公差d = -2, 为其前n项和.若
为其前n项和.若 ,则
,则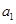 =
= }的前n项和为Sn,且
}的前n项和为Sn,且 的最小值为 .
的最小值为 . ,求证:
,求证: ;
; ,写出
,写出 并猜想这个数列的通项公式达式.
并猜想这个数列的通项公式达式. 的第二项为8,前10项和为185。
的第二项为8,前10项和为185。 项,……按原来顺序组成一个新
项,……按原来顺序组成一个新 数列,试求数列
数列,试求数列