题目内容
设{ }为等差数列,公差d = -2,
}为等差数列,公差d = -2, 为其前n项和.若
为其前n项和.若 ,则
,则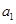 =
=
 }为等差数列,公差d = -2,
}为等差数列,公差d = -2, 为其前n项和.若
为其前n项和.若 ,则
,则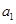 =
=| A.18 | B.20 | C.22 | D.24 |
B
试题分析:由等差数列的前10项的和等于前11项的和可知,第11项的值为0,然后根据等差数列的通项公式,利用首项和公差d表示出第11项,让其等于0列出关于首项的方程,求出方程的解即可得到首项的值.解:由s10=s11,得到a1+a2+…+a10=a1+a2+…+a10+a11即a11=0,所以a1-2(11-1)=0,解得a1=20.故选B
点评:此题考查学生掌握等差数列的性质,灵活运用等差数列的通项公式化简求值,是一道基础题

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
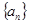 中,已知
中,已知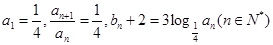 .
.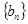 是等差数列;
是等差数列;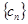 满足
满足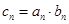 ,求
,求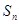 .
. 的前
的前 项和为
项和为 的值( )
的值( ) 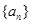 满足:
满足: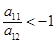 ,且公差
,且公差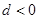 ,其前
,其前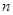 项和为
项和为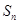 .则满足
.则满足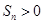 的
的



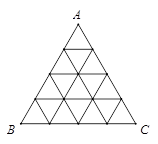
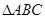 分割成16个全等的小正三角形,在每个三角形的顶点各放置一个数,使位于同一直线上的点放置的数(当数的个数不少于3时)都分别依次成等差数列,若顶点
分割成16个全等的小正三角形,在每个三角形的顶点各放置一个数,使位于同一直线上的点放置的数(当数的个数不少于3时)都分别依次成等差数列,若顶点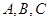 处的三个数互不相同且和为1,则所有顶点的数之和
处的三个数互不相同且和为1,则所有顶点的数之和 .
.
 中,
中, ,则
,则 =( )
=( ) 在函数
在函数 图象上,过点
图象上,过点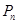 的切线的方向向量为
的切线的方向向量为 (
( >0).
>0). 的通项公式
的通项公式 ≤Sn对任意正整数n均成立,求实数
≤Sn对任意正整数n均成立,求实数