题目内容
数列{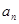 }的前n项和为
}的前n项和为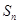 ,
,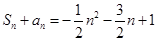 ,
,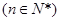 .
.
(1)设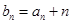 ,证明:数列
,证明:数列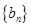 是等比数列;
是等比数列;
(2)求数列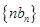 的前
的前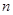 项和
项和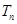 ;
;
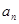 }的前n项和为
}的前n项和为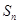 ,
,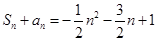 ,
,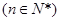 .
.(1)设
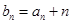 ,证明:数列
,证明:数列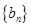 是等比数列;
是等比数列;(2)求数列
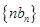 的前
的前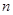 项和
项和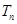 ;
;(1)根据题意,由于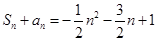 ,那么可知
,那么可知 递推关系式,进而得到证明。
递推关系式,进而得到证明。
(2)
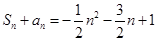 ,那么可知
,那么可知 递推关系式,进而得到证明。
递推关系式,进而得到证明。(2)

试题分析:(1) 因为
 ,
,所以 ① 当
 时,
时, ,则
,则 , 1分
, 1分② 当
 时,
时, , 2分
, 2分所以
 ,即
,即 ,
,所以
 ,而
,而 , 4分
, 4分所以数列
 是首项为
是首项为 ,公比为
,公比为 的等比数列,所以
的等比数列,所以 . 6分
. 6分(2)由(1)得
 .
.所以 ①
 ,
,②
 , 8分
, 8分②-①得:
 , 10分
, 10分 . 12分
. 12分点评:主要是考查了递推关系式和数列求和的运用,属于基础题。

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
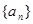 满足
满足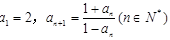 ,则该数列的前2013项的乘积______.
,则该数列的前2013项的乘积______. 的前
的前 项和为
项和为 ,且
,且 ,
, .
. 的前
的前 ,且
,且 (
( 为常数),令
为常数),令 ,求数列
,求数列 的前
的前 。
。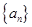 的公差
的公差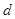 =1,前
=1,前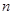 项和为
项和为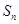 .
.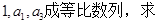
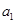 ;
;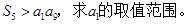
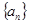 中,已知
中,已知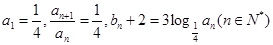 .
.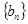 是等差数列;
是等差数列;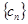 满足
满足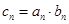 ,求
,求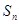 .
. 是等差数列,其前
是等差数列,其前 项和为
项和为 ,若
,若 ,
, ,则
,则 ( )
( )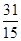
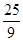

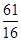
 的一个内角为
的一个内角为 ,并且三边构成公差为4的等差数列,那么
,并且三边构成公差为4的等差数列,那么


