题目内容
11.讨论函数f(x)=|x-2|+ax+a-1(a∈R)的零点个数.分析 作函数y=|x-2|-1与y=-a(x+1)的图象,由数形结合求得.
解答 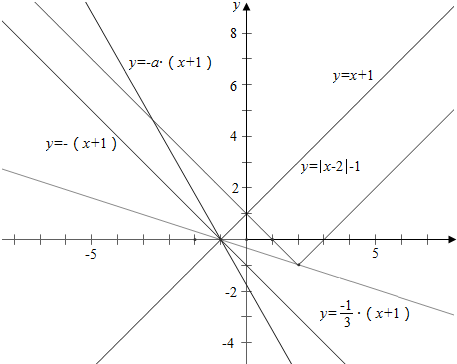 解:令y=|x-2|-1,y=-a(x+1);
解:令y=|x-2|-1,y=-a(x+1);
作函数y=|x-2|-1与y=-a(x+1)的图象如右图,
结合图象可知,
当-a=-$\frac{1}{3}$,即a=$\frac{1}{3}$时,函数y=|x-2|-1与y=-a(x+1)的图象有一个交点,
当-$\frac{1}{3}$<-a<1,即-1<a<$\frac{1}{3}$时,
函数y=|x-2|-1与y=-a(x+1)的图象有两个交点,
当-a≥1或-a<-1,即a≤-1或a>1时,
函数y=|x-2|-1与y=-a(x+1)的图象有一个交点,
当-1≤-a<-$\frac{1}{3}$,即$\frac{1}{3}$<a≤1时,
函数y=|x-2|-1与y=-a(x+1)的图象没有交点,
综上所述,
当a≤-1或a>1或a=$\frac{1}{3}$时,
函数f(x)=|x-2|+ax+a-1(a∈R)有一个零点,
当-1<a<$\frac{1}{3}$时,
函数f(x)=|x-2|+ax+a-1(a∈R)有两个零点,
当$\frac{1}{3}$<a≤1时,
函数f(x)=|x-2|+ax+a-1(a∈R)没有零点.
点评 本题考查了函数的零点与函数的图象的交点的关系应用,同时考查了数形结合的思想应用.

练习册系列答案
相关题目
20.f(cosx)=cos2x,那么f(sin150°)的值为 ( )
| A. | -1 | B. | 1 | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
1.已知某次期中考试中,甲、乙两组学生的数学成绩如下:
甲:88 100 95 86 95 91 84 74 92 83
乙:93 89 81 77 96 78 77 85 89 86
则下列结论正确的是( )
甲:88 100 95 86 95 91 84 74 92 83
乙:93 89 81 77 96 78 77 85 89 86
则下列结论正确的是( )
| A. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,s甲>s乙 | B. | ${\overline{x}}_{甲}$>${\overline{x}}_{乙}$,s甲<s乙 | ||
| C. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,s甲>s乙 | D. | ${\overline{x}}_{甲}$<${\overline{x}}_{乙}$,s甲<s乙 |