题目内容
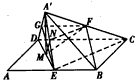
如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°,E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,F为线段A′C的中点.
(Ⅰ)求证:BF∥平面A′DE;
(Ⅱ)设M为线段DE的中点,求直线FM与平面A′DE所成角的余弦值.
(Ⅰ)求证:BF∥平面A′DE;
(Ⅱ)设M为线段DE的中点,求直线FM与平面A′DE所成角的余弦值.
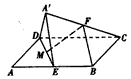
| (Ⅰ)证明:取A'D的中点G,连结GF,GE, 由条件易知 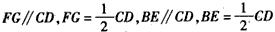 , ,所以FC∥BE,FG=BE, 故四边形BEGF为平行四边形, 所以BF∥EG, 因为EG 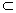 平面A′DE,BF 平面A′DE,BF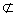 平面A′DE, 平面A′DE,所以BF∥平面A′DE。 (Ⅱ)在平行四边形ABCD中,设BC=a, 则AB=CD=2a,AD=AE=EB=a,连结CE, 因为∠ABC=120°, 在△BCE中,可得CE=a, 在△ADE中,可得DE=a, 在△CDE中,因为CD2=CE2+DE2,所以CE⊥DE, 在正三角形A′DE中,M为DE中点,所以A′M⊥DE, 由平面A′DE⊥平面BCD,可知A′M⊥平面BCD,A′M⊥CE, 取A′E的中点N,连结NM,NF, 所以NF⊥DE,NF⊥A′M, 因为DE交A′M于M,所以NF⊥平面A′DE, 则∠FMN为直线FM与平面A′DE所成角, 在Rt△FMN中, 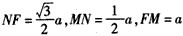 , ,则 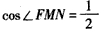 , , 所以直线FM与平面A′DE所成角的余弦值为 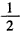 。 。 |
 |

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,下列结论中错误的是( )
如图,在平行四边形ABCD中,下列结论中错误的是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
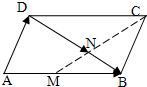 如图,在平行四边形ABCD,
如图,在平行四边形ABCD, 如图,在平行四边形ABCD中,
如图,在平行四边形ABCD中,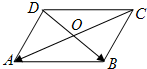 如图,在平行四边形ABCD中,若
如图,在平行四边形ABCD中,若 如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的中点.
如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的中点.