已知复数z=$\frac{1+ai}{1-i}$的虚部为1.则a=( )A．1B．-1C．-2D．2 题目和参考答案——青夏教育精英家教网—

题目内容

6．已知复数z=$\frac{1+ai}{1-i}$（a∈R）的虚部为1，则a=（　　）

A．

B．

-1

C．

-2

D．

分析利用复数的运算法则、虚部的定义即可得出．

解答解：复数z=$\frac{1+ai}{1-i}$=$\frac{（1+ai）（1+i）}{（1-i）（1+i）}$=$\frac{1-a}{2}$+$\frac{a+1}{2}$i（a∈R）的虚部为1，
∴$\frac{a+1}{2}$=1，解得a=1．
故选：A．

点评本题考查了复数的运算法则、虚部的定义，考查了推理能力与计算能力，属于基础题．

练习册系列答案

相关题目

已知函数f（x）＝asin（πx＋α）＋bcos（πx＋β），且f（3）＝3，则f（2 016）＝________．

17．已知两定点A（-2，0），B（1，0），若圆心在直线x-y-1=0上且半径为1的动圆P上存在一点Q满足|QA|=2|QB|，则点P横坐标a的取值范围为$\frac{3-\sqrt{17}}{2}≤a≤1$或2≤a≤$\frac{3+\sqrt{17}}{2}$．

14．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的图象与直线y=b（0＜b＜A）的三个相邻交点的横坐标分别是1，2，4，则f（x）的单调递增区间是（　　）

A．

[3k-$\frac{3}{2}$，3k]，k∈Z

B．

[3k，3k+$\frac{3}{2}$]，k∈Z

C．

[3kπ-$\frac{3}{2}$，3kπ]，k∈Z

D．

[3kπ，3kπ+$\frac{3}{2}$]，k∈Z

1．如图，是一个几何体的三视图，则此几何体的外接球的半径为（　　）

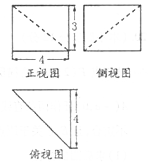
A．

$\frac{\sqrt{34}}{2}$

B．

$\frac{\sqrt{41}}{2}$

C．

D．

11．已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|≤$\frac{π}{2}$）的最小正周期为π，且x=$\frac{π}{12}$为f（x）图象的一条对称轴．
（1）求ω和φ的值；
（2）设函数g（x）=f（x）+f（x-$\frac{π}{6}$），求g（x）的单调递减区间．

18．过双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点F作x轴的垂线，交双曲线C于M，N两点，A为左顶点，设∠MAN=θ，双曲线C的离心率为f（θ），则f（$\frac{2π}{3}$）-f（$\frac{π}{3}$）等于（　　）

A．

$\frac{2\sqrt{3}}{3}$

X	1	2	3
P	P₁	P₂	P₃

P₁=P₂

P₂=P₃

P₁=P₃

P₁=P₂=P₃

已知，则的值是（）

A． B．9 C． D．

试题分类