题目内容
14.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与直线y=b(0<b<A)的三个相邻交点的横坐标分别是1,2,4,则f(x)的单调递增区间是( )| A. | [3k-$\frac{3}{2}$,3k],k∈Z | B. | [3k,3k+$\frac{3}{2}$],k∈Z | C. | [3kπ-$\frac{3}{2}$,3kπ],k∈Z | D. | [3kπ,3kπ+$\frac{3}{2}$],k∈Z |
分析 三角函数的图象与直线y=b(0<b<A)的三个相邻交点的横坐标分别是1,2,4,至少提供两个方面的信息:
①第一个交点与第三个交点的差是一个周期;
②第一个交点与第二个交点的中点横坐标对应的函数值是最大值或最小值;
从这两个方面考虑求得参数ω,φ,从而利用三角函数的单调性求答案.
解答 解:与直线y=b(0<b<A)的三个相邻交点的横坐标分别是1,2,4,
知函数的周期为T=$\frac{2π}{ω}$=4-1=3,
解得ω=$\frac{2π}{3}$;
再由三角函数的图象与直线y=b(0<b<A)知:
1与2的中点必为函数的最大值的横坐标,
由五点法知$\frac{2π}{3}$×$\frac{3}{2}$+φ=$\frac{π}{2}$,
解得φ=-$\frac{π}{2}$;
∴f(x)=Asin($\frac{2π}{3}$x-$\frac{π}{2}$)=-Acos($\frac{2π}{3}$x),
令2kπ≤$\frac{2π}{3}$x≤2kπ+π,k∈Z,
解得3k≤x≤3k+$\frac{3}{2}$,k∈Z,
∴f(x)的单调递增区间是[3k,3k+$\frac{3}{2}$],(k∈Z).
故选:B.
点评 本题考查了三角函数的解析式以及三角函数的图象与性质的应用问题,是综合性题目.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
9.已知全集U={1,2,3},集合A={1},B={2},则∁U(A∪B)=( )
| A. | ∅ | B. | U | C. | {1,2} | D. | {3} |
19.已知全集U=R,A={x|x2>1},∁UA=( )
| A. | [-1,1] | B. | (-∞,1) | C. | (-1,1) | D. | (-∞,1] |
6.已知复数z=$\frac{1+ai}{1-i}$(a∈R)的虚部为1,则a=( )
| A. | 1 | B. | -1 | C. | -2 | D. | 2 |
3.《数学九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白,与著名的海伦公式完全等价,由此可以看出我国古代已具有很高的数学水平,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂减上,余四约之,为实.一为从隔,开平方得积.”若把以上这段文字写成公式,即S=$\sqrt{\frac{1}{4}[{c}^{2}{a}^{2}-(\frac{{c}^{2}+{a}^{2}-{b}^{2}}{2})^{2}]}$.现有周长为2$\sqrt{2}$+$\sqrt{5}$的△ABC满足sinA:sinB:sinC=($\sqrt{2}$-1):$\sqrt{5}$:($\sqrt{2}$+1),试用以上给出的公式求得△ABC的面积为( )
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{5}}{4}$ | D. | $\frac{\sqrt{5}}{2}$ |
 ,P(N)=
,P(N)=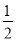
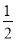 ,P(N)=
,P(N)=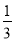 ,P(N)=
,P(N)=