题目内容
16.正四面体的棱长为a,它的顶点都在同一球面上,则这个球的表面积是( )| A. | 3πa2 | B. | 2πa2 | C. | $\frac{3π{a}^{2}}{2}$ | D. | $\frac{π{a}^{2}}{3}$ |
分析 由已知中正四面体的棱长为a,我们计算出其外接球的半径,代入球的表面积公式,即可得到答案.
解答 解:正四面体扩充为正方体,若正四面体的棱长为a,则正方体的棱长为$\frac{\sqrt{2}}{2}$a,
所以正方体的对角线长为$\frac{\sqrt{6}}{2}$a,
则正四面体的外接球半径为$\frac{\sqrt{6}}{4}$a
所以其外接球的表面积S=4πR2=$\frac{3π{a}^{2}}{2}$.
故选:C.
点评 本题考查的知识点是球的表面积,其中根据已知计算出四面体的外接球半径是解答本题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
7.阅读如图的程序框图,运行相应的程序,输出n的值为( )


| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
1.若点P(1,2)在以坐标原点为圆心的圆上,则该点在点P处的切线方程是( )
| A. | x+2y-5=0 | B. | x-2y+3=0 | C. | 2x+y-4=0 | D. | 2x-y=0 |
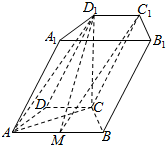 如图所示,在四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,∠DAB=60°,AB=2CD=2,若CD1垂直于平面ABCD,且$C{D_1}=\sqrt{3}$,M是线段AB的中点.
如图所示,在四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,∠DAB=60°,AB=2CD=2,若CD1垂直于平面ABCD,且$C{D_1}=\sqrt{3}$,M是线段AB的中点.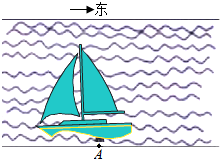 为了调运急需物资,如图所示,一艘船从长江南岸A点出发,以5$\sqrt{3}$km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东5km/h.
为了调运急需物资,如图所示,一艘船从长江南岸A点出发,以5$\sqrt{3}$km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东5km/h.