Question

6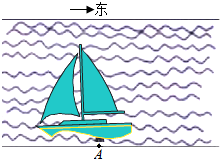．为了调运急需物资，如图所示，一艘船从长江南岸A点出发，以5$\sqrt{3}$km/h的速度向垂直于对岸的方向行驶，同时江水的速度为向东5km/h．
（1）试用向量表示江水的速度、船速以及船实际航行的速度；
（2）求船实际航行的速度的大小与方向（用与江水的速度方向间的夹角表示）．

Answer 1

分析 （1）根据方向和速度大小作图；（2）利用向量加法的平行四边形法则求出矩形的对角线和∠DAC．

解答 解：（1）作出向量如图所示：

其中$\overrightarrow{AC}$表示江水速度，$\overrightarrow{AB}$表示船速，$\overrightarrow{AD}$表示船实际航行速度．
（2）∵AB⊥AC，$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{AC}$，∴四边形ABDC是矩形，
∴|$\overrightarrow{AD}$|=$\sqrt{{5}^{2}+（5\sqrt{3}）^{2}}$=10．tan∠DAC=$\frac{5\sqrt{3}}{5}$=$\sqrt{3}$，∴∠DAC=60°．
∴船实际航行的速度为10km/h，实际航行方向与江水速度方向夹角为60°．

点评 本题考查了平面向量线性运算的几何意义，属于基础题．