题目内容
9.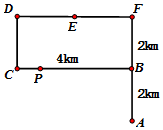 8月27日我校组织了高一学生拉练活动,步行路线如图:A→B→C→D→E→F→A(A是学校,BCDF为矩形,AB=BF=2km,BC=4km),步行匀速前进,速度4km/h,拉练过程中在DF的中点E处休息了半小时,从学校A点出发开始计时,经过t小时到达P点,P到A的直线距离为|PA|,设y=|PA|2.
8月27日我校组织了高一学生拉练活动,步行路线如图:A→B→C→D→E→F→A(A是学校,BCDF为矩形,AB=BF=2km,BC=4km),步行匀速前进,速度4km/h,拉练过程中在DF的中点E处休息了半小时,从学校A点出发开始计时,经过t小时到达P点,P到A的直线距离为|PA|,设y=|PA|2.(1)写出y关于t的函数的定义域、值域.
(2)写出y关于t的函数表达式.
分析 (1)由题意,$\frac{18}{4}$=$\frac{9}{2}$,|AD|=4$\sqrt{2}$,即可写出y关于t的函数的定义域、值域.
(2)分类讨论,即可写出y关于t的函数表达式.
解答 解:(1)由题意,$\frac{18}{4}$=$\frac{9}{2}$,∴函数的定义域为[0,$\frac{9}{2}$],|AD|=4$\sqrt{2}$,∴值域为[0,32].
(2)当0≤t≤$\frac{1}{2}$时,y=16t2,
当$\frac{1}{2}<t≤\frac{3}{2}$时,y=4+$[4(t-\frac{1}{2})]^{2}$=16(t-$\frac{1}{2}$)2+4,
当$\frac{3}{2}$<t≤2时,y=16+[2+4(t-$\frac{3}{2}$)]2=16(t-1)2+16
当2<t≤$\frac{5}{2}$时,y=16+[4-4(t-2)]2=16(t-3)2+16,
当$\frac{5}{2}$<t≤3时,y=16+4=20,
当3<t≤$\frac{7}{2}$时,y=16+[2-4(t-3)]2=16(t-$\frac{7}{2}$)2+16,
当$\frac{7}{2}$<t≤$\frac{9}{2}$时,y=[4-4(t-$\frac{7}{2}$)]2=16(t-$\frac{9}{2}$)2.
点评 本题考查利用数学知识解决实际问题,考查分段函数,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
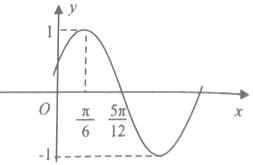 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示, 倾斜角$\frac{π}{4}$的直线l过抛物线y2=4x焦点,且与抛物线相交于A、B两点.
倾斜角$\frac{π}{4}$的直线l过抛物线y2=4x焦点,且与抛物线相交于A、B两点.