题目内容
17.在极坐标系中,圆C的方程为ρ=4cosθ,以极点为坐标原点,极轴为x轴的非负半轴建立平面直角坐标系,直线l经过点M(5,6),且斜率为$\frac{4}{3}$.(1)求圆 C的平面直角坐标方程和直线l的参数方程;
(2)若直线l与圆C交于A,B两点,求|MA|+|MB|的值.
分析 (1)由ρ2=x2+y2,ρcosθ=x,能求出圆C的平面直角坐标方程,由直线l经过点M(5,6),且斜率为$\frac{4}{3}$,能求出直线l的参数方程.
(2)把直线l的参数方程代入圆C:(x-2)2+y2=4,得5t2+66t+205=0,由此能求出|MA|+|MB|的值.
解答 解:(1)∵圆C的方程为ρ=4cosθ,∴ρ2=4ρcosθ,
∵ρ2=x2+y2,ρcosθ=x,
∴圆C的平面直角坐标方程为:(x-2)2+y2=4,
∵直线l经过点M(5,6),且斜率为$\frac{4}{3}$,
∴tanθ=$\frac{4}{3}$,cos$θ=\frac{3}{5}$,sinθ=$\frac{4}{5}$,
∴直线l的参数方程为$\left\{\begin{array}{l}x=5+\frac{3}{5}t\\ y=6+\frac{4}{5}t\end{array}\right.(t$为参数 ).
(2)把直线l的参数方程代入圆C:(x-2)2+y2=4,
得:5t2+66t+205=0,
∴$|{MA}|+|{MB}|=|{t_1}|+|{t_2}|=|{{t_1}+{t_2}}|=\frac{66}{5}$.
点评 本题考查圆的直角坐标方程、直线的参数方程的求法,考查两线段和的求法,考查极坐标方程、参数方程、直角坐标方程等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、化归与转化思想,是中档题.

练习册系列答案
相关题目
8.已知向量$\overrightarrow{AB}=(2,-1)$,$\overrightarrow{BC}=(-4,1)$,向量$\overrightarrow{AC}$的坐标是( )
| A. | (-6,2) | B. | (6,-2) | C. | (-2,0) | D. | (2,0) |
8.已知命题p1:?x0∈R,x02+x0+1<0;p2:?x∈[1,2],x2-1≥0.以下命题为真命题的是( )
| A. | (¬p1)∧(¬p2) | B. | p1∨(¬p2) | C. | (¬p1)∧p2 | D. | p1∧p2 |
12.已知sinα=$\frac{3}{5}$$(\frac{π}{2}<α<π)$,则$sin(α-\frac{π}{3})$=( )
| A. | $\frac{{4\sqrt{3}-3}}{10}$ | B. | $\frac{{4\sqrt{3}+3}}{10}$ | C. | $\frac{{3-4\sqrt{3}}}{10}$ | D. | $\frac{{4\sqrt{3}+3}}{5}$ |
2.若a是从区间[0,3]中任取的一个实数,则1<a<2的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
9.根据如图的流程图,可得的结果是( )
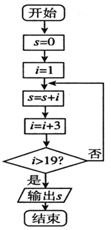

| A. | 76 | B. | 70 | C. | 51 | D. | 19 |
5.函数y=xex的导数是( )
| A. | y=xex | B. | y=x+xex | C. | y=ex | D. | y=(1+x)ex |