题目内容
3.已知双曲线C:$\frac{x^2}{9}-\frac{y^2}{4}$=1,点M与曲线C的焦点不重合,若点M关于曲线C的两个焦点的对称点分别为A,B,M,N是坐标平面内的两点,且线段MN的中点P恰好在双曲线C上,则|AN-BN|=12.分析 根据已知条件,作出图形,MN的中点连接双曲线的两个焦点,便会得到三角形的中位线,根据中位线的性质及双曲线上的点到两焦点的距离之差的绝对值为2a,即可求出||AN|-|BN||.
解答 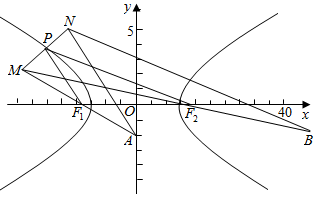 解:双曲线C:$\frac{x^2}{9}-\frac{y^2}{4}$=1的a=3,
解:双曲线C:$\frac{x^2}{9}-\frac{y^2}{4}$=1的a=3,
设双曲线C的左右焦点分别为F1,F2,如图,
连接PF1,PF2,
∵F1是MA的中点,P是MN的中点,
∴F1P是△MAN的中位线,
∴|PF1|=$\frac{1}{2}$|AN|,
同理|PF2|=$\frac{1}{2}$|BN|,
∴||AN|-|BN||=2||PF1|-|PF2||,
∵P在双曲线上,
根据双曲线的定义知:
||PF1|-|PF2||=2a=6,
∴||AN|-|BN||=12.
故答案为:12.
点评 本题考查双曲线的定义、方程和性质,同时考查三角形的中位线,运用定义法是解题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}={1^{\;}}({a>b>0})$右焦点作双曲线其中一条渐近线的垂线与两渐近线分别交于A,B两点,O为坐标原点,且△AOB的面积为$\frac{{6{a^2}}}{5}$,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{5}}}{3}$ | C. | $\frac{{\sqrt{13}}}{2}$ | D. | $\frac{{\sqrt{13}}}{3}$ |
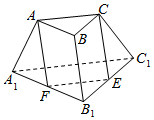 在三棱台ABC-A1B1C1中,A1B1=2AB,点E、F分别是棱B1C1、A1B1的中点,则在三棱台的各棱所在的直线中,与平面ACEF平行的有A1C1、BB1.
在三棱台ABC-A1B1C1中,A1B1=2AB,点E、F分别是棱B1C1、A1B1的中点,则在三棱台的各棱所在的直线中,与平面ACEF平行的有A1C1、BB1.