题目内容
18．
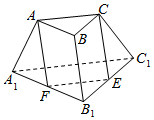在三棱台ABC-A1B1C1中，A1B1=2AB，点E、F分别是棱B1C1、A1B1的中点，则在三棱台的各棱所在的直线中，与平面ACEF平行的有A1C1、BB1．
分析 由中位线定理可知EF∥A1C1，故A1C1∥平面ACEF，由AB$\stackrel{∥}{=}$FB1得四边形ABB1F是平行四边形，故AF∥BB1，所以BB1∥平面ACEF．
解答 解：∵点E、F分别是棱B1C1、A1B1的中点，
∴EF∥A1C1，又EF?平面ACEF，A1C1?平面ACEF，
∴A1C1∥平面ACEF．
∵AB∥A1B1，A1B1=2AB，FB1=$\frac{1}{2}$A1B1，
∴AB$\stackrel{∥}{=}$FB1，
∴四边形ABB1F是平行四边形，
∴AF∥BB1，又AF?平面ACEF，BB1?平面ACEF，
∴BB1∥平面ACEF．
故答案为：A1C1，BB1．
点评 本题考查了平面平行的判定，属于基础题．
练习册系列答案
阶梯计算系列答案
相关题目
9．（普通中学做）已知双曲线C1：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）以及双曲线C2：$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的渐近线将第一象限三等分，则C1，C2的离心率之积为（ ）
| A． | $\frac{4\sqrt{3}}{3}$ | B． | $\frac{4}{3}$或4 | C． | $\frac{4}{3}$ | D． | 4 |
10．已知F1（-1，0），F2（1，0）是椭圆C1与双曲线C2共同的焦点，椭圆的一个短轴端点为B，直线F1B与双曲线的一条渐近线平行，椭圆C1与双曲线C2的离心率分别为e1，e2，则e1+e2取值范围为（ ）
| A． | [2，+∞） | B． | [4，+∞） | C． | （4，+∞） | D． | （2，+∞） |
7．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的一个焦点恰为抛物线y2=8x的焦点，且离心率为2，则该双曲线的标准方程为（ ）
| A． | ${x^2}-\frac{y^2}{3}=1$ | B． | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | C． | $\frac{x^2}{3}-{y^2}=1$ | D． | $\frac{x^2}{12}-\frac{y^2}{4}=1$ |