题目内容
在一个盒中装有6枝圆珠笔,其中3枝一等品,2枝二等品和1枝三等品,从中任取两枝.
(1)求恰有1枝一等品的概率;
(2)求没有三等品的概率.
(1)求恰有1枝一等品的概率;
(2)求没有三等品的概率.
考点:列举法计算基本事件数及事件发生的概率,分层抽样方法
专题:概率与统计
分析:对题目中的样品进行编号,用列举法求出基本事件数,再计算对应的概率即可.
解答:
解:(1)记一等品为a、b、b,二等品为d、e,三等品为f,
从中任取2枝的所有可能为
ab、ac、ad、ae、af、bc、bd、be、bf、cd、ce、cf、de、df、ef共15种,
恰有1枝一等品的取法为
ad、ae、af、bd、be、bf、cd、ce、cf共9种,
∴恰有1枝一等品的概率为P=
=
;
(2)没有三等品的取法有
ab、ac、ad、ae、bc、bd、be、cd、ce、de共10种,
∴没有三等品的概率为P=
=
.
从中任取2枝的所有可能为
ab、ac、ad、ae、af、bc、bd、be、bf、cd、ce、cf、de、df、ef共15种,
恰有1枝一等品的取法为
ad、ae、af、bd、be、bf、cd、ce、cf共9种,
∴恰有1枝一等品的概率为P=
| 9 |
| 15 |
| 3 |
| 5 |
(2)没有三等品的取法有
ab、ac、ad、ae、bc、bd、be、cd、ce、de共10种,
∴没有三等品的概率为P=
| 10 |
| 15 |
| 2 |
| 3 |
点评:本题考查了用列举法得出基本事件数,从而计算出对应的概率的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,设全集U=R,M={x|x>2},N={0,1,2,3},则图中阴影部分所表示的集合是( )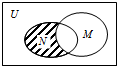

| A、{3} |
| B、{0,1} |
| C、{0,1,2} |
| D、{0,1,2,3} |
 已知函数f(x)=Asin(ωx-
已知函数f(x)=Asin(ωx-| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
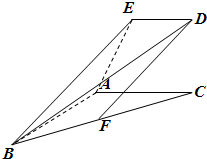 如图所示,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,AB=AC=AE=2ED=2a,F是BC的中点.
如图所示,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,AB=AC=AE=2ED=2a,F是BC的中点.