题目内容
计算定积分:
(1)
e2xdx;
(2)
cos2xdx;
(3)
2xdx.
(1)
| ∫ | 1 0 |
(2)
| ∫ |
|
(3)
| ∫ | 3 1 |
考点:定积分
专题:导数的概念及应用
分析:根据定积分的计算法则计算即可.
解答:
解:(1)
e2xdx=
e2x|
=
e2-
(2)
cos2xdx=
sin2x
=
(sin
-sin
)=
-
(3)
2xdx=
2x
=
×(8-2)=
| ∫ | 1 0 |
| 1 |
| 2 |
1 0 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)
| ∫ |
|
| 1 |
| 2 |
| | |
|
| 1 |
| 2 |
| π |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 4 |
(3)
| ∫ | 3 1 |
| 1 |
| ln2 |
| | | 3 1 |
| 1 |
| ln2 |
| 6 |
| ln2 |
点评:本题考查了定积分的计算,关键是求出原函数,属于基础题.

练习册系列答案
相关题目
圆锥的底面半径为1,母线长为3,则圆锥的表面积为( )
| A、π | B、2π | C、3π | D、4π |
圆锥的母线长为2,侧面展开图是一个半圆,则此圆锥的表面积为( )
| A、6π | B、5π | C、3π | D、2π |
圆柱的侧面展开图是正方形,则它的侧面积与下底面积的比值是( )
| A、3π | B、4 | C、3 | D、4π |
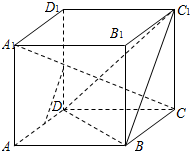 如图,在正方体ABCD-A1B1C1D1中,E,F分别是AD,DD1中点.求证:(1)EF∥平面C1BD;
如图,在正方体ABCD-A1B1C1D1中,E,F分别是AD,DD1中点.求证:(1)EF∥平面C1BD;