题目内容
11. 已知f(x)是R上的奇函数,且当x>0时,f(x)=-x2+2x+3,
已知f(x)是R上的奇函数,且当x>0时,f(x)=-x2+2x+3,(Ⅰ)求f(x)的表达式;
(Ⅱ)在所给的坐标系中画出f(x)的草图(要求:要标出与坐标轴的交点,顶点),然后写出f(x)的单调区间;
(Ⅲ)若函数y=a的图象与y=f(x)的图象恰有两个交点,求实数a的取值范围?
分析 (Ⅰ)利用函数奇偶性的性质即可求f(x)的表达式;
(Ⅱ)根据分段函数结合一元二次函数的图象和性质进行求解即可;
(Ⅲ)利用数形结合进行求解即可.
解答 解:(Ⅰ)∵f(x)是R上的奇函数,且当x>0时,f(x)=-x2+2x+3,
∴f(0)=0,
当x<0,则-x>0,即f(-x)=-x2-2x+3=-f(x),
即f(x)=x2+2x-3,x<0,
即f(x)=$\left\{\begin{array}{l}{-{x}^{2}+2x+3,}&{x>0}\\{0}&{x=0}\\{{x}^{2}+2x-3,}&{x<0}\end{array}\right.$.
(Ⅱ)在所给的坐标系中画出f(x)的草图如图:
则f(x)的单调增区间为:[-1,0);(0,1].
单调递减区间为(-∞,-1];[1,+∞)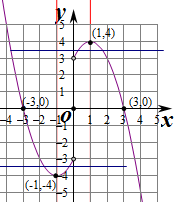 .
.
(Ⅲ)若函数y=a的图象与y=f(x)的图象恰有两个交点,
则由图象知a=4或a=-4或-3≤a≤3.
点评 本题主要考查函数奇偶性的应用,以及函数解析式的求解,利用函数奇偶性的对称性结合一元二次函数的图象和性质是解决本题的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
3.对于函数f(x),若?a,b,c∈R,f(a),f(b),f(c)都是某一三角形的三边长,则称f(x)为“可构造三角形函数”.以下说法正确的是( )
| A. | f(x)=8(x∈R)不是“可构造三角形函数” | |
| B. | “可构造三角形函数”一定是单调函数 | |
| C. | f(x)=$\frac{1}{{x}^{2}+1}$(x∈R)是“可构造三角形函数” | |
| D. | 若定义在R上的函数f(x)的值域是[$\sqrt{e}$,e](e为自然对数的底数),则f(x)一定是“可构造三角形函数” |
20.若函数f(x)=$\frac{1}{\sqrt{lo{g}_{0.2}(2x-1)}}$,则函数f(x)的定义域为( )
| A. | ($\frac{1}{2}$,+∞) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{1}{2}$,1] | D. | (-$\frac{1}{2}$,0) |