题目内容
(本小题满分13分)已知函数 和
和 的图象有公共点P,且在点P处的切线相同.
的图象有公共点P,且在点P处的切线相同.
(Ⅰ)若点P的坐标为 ,求
,求 的值;
的值;
(Ⅱ)已知 ,求切点P的坐标.
,求切点P的坐标.
(Ⅰ) ,
, ; (Ⅱ)
; (Ⅱ)
【解析】
试题分析:(Ⅰ)由题意,得 ,且
,且 ,
, , 由已知,得
, 由已知,得 ,即
,即 ,解方程,即可求出结果.(Ⅱ)若
,解方程,即可求出结果.(Ⅱ)若 ,则
,则 ,
, ,设切点坐标为
,设切点坐标为 ,其中
,其中 ,由题意,得
,由题意,得  ①,
①, ②,由②,得
②,由②,得 ,其中
,其中 ,代入①,得
,代入①,得  (*),因为
(*),因为  ,且
,且 ,所以
,所以  .设函数
.设函数  ,
, ,
,
则  ,令
,令 ,解得
,解得 或
或 (舍). 列出当
(舍). 列出当 变化时,
变化时, 与
与 的变化情况表,解方程即可求出切点P的坐标.
的变化情况表,解方程即可求出切点P的坐标.
试题解析:(Ⅰ)【解析】
由题意,得 , 1分
, 1分
且 ,
, , 3分
, 3分
由已知,得 ,即
,即 ,
,
解得 ,
, . 5分
. 5分
(Ⅱ)【解析】
若 ,则
,则 ,
, ,
,
设切点坐标为 ,其中
,其中 ,
,
由题意,得  , ①
, ①
 , ② 6分
, ② 6分
由②,得  ,其中
,其中 ,
,
代入①,得  . (*) 7分
. (*) 7分
因为  ,且
,且 ,
,
所以  . 8分
. 8分
设函数  ,
, ,
,
则  . 9分
. 9分
令 ,解得
,解得 或
或 (舍). 10分
(舍). 10分
当 变化时,
变化时, 与
与 的变化情况如下表所示,
的变化情况如下表所示,
|
| 1 |
|
|
| 0 |
|
| ↗ | ↘ |
12分
所以当 时,
时, 取到最大值
取到最大值 ,且当
,且当 时
时 .
.
因此,当且仅当 时
时 .
.
所以方程(*)有且仅有一解 .
.
于是  ,
,
因此切点P的坐标为 . 13分.
. 13分.
考点:1.导数的几何意义;2.导数在函数单调性上的应用.







 ,满足对任意的
,满足对任意的 ,均有
,均有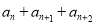 为定值.若
为定值.若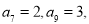
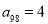 ,则数列
,则数列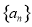 的前100项的和
的前100项的和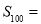 ( ).
( ). 满足
满足 ,
, ,
, ,那么
,那么 ____.
____. ABC中,角A,B,C所对的边分别为a,b,c. 若
ABC中,角A,B,C所对的边分别为a,b,c. 若 ,
, ,则( )
,则( ) (B)
(B)
 (D)
(D)
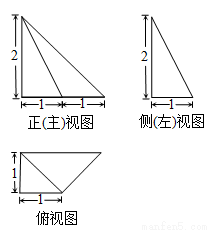
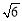
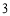
 )如图所示,则该棱锥的体积等于
)如图所示,则该棱锥的体积等于  。
。
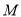 在曲线
在曲线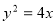 上”是“点
上”是“点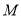 的坐标满足方程
的坐标满足方程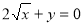 ”的( )
”的( )