题目内容
12.某四棱锥的三视图如图所示,则该四棱锥的四个侧面的面积中最大值是6.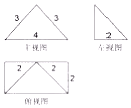
分析 由三视图得几何体是四棱锥并画出直观图,由三视图判断出线面的位置关系,并求出几何体的高和侧面的高,分别求出各个侧面的面积,即可得到答案.
解答 解:由三视图得几何体是四棱锥P-ABCD, 如图所示:
如图所示:
且PE⊥平面ABCD,底面ABCD是矩形,AB=4、AD=2,
面PDC是等腰三角形,PD=PC=3,
则△PDC的高为$\sqrt{9-4}$=$\sqrt{5}$,
所以△PDC的面积为:$\frac{1}{2}$×4×$\sqrt{5}$=2$\sqrt{5}$,
因为PE⊥平面ABCD,所以PE⊥BC,
又CB⊥CD,PE∩CD=E,所以BC⊥面PDC,
即BC⊥PC,同理可证AD⊥PD,
则两个侧面△PAD、△PBC的面积都为:$\frac{1}{2}$×2×3=3,
侧面△PAB的面积为:$\frac{1}{2}$×4×$\sqrt{5+4}$=6,
所以四棱锥P-ABCD的四个侧面中面积最大是:6,
故答案为6.
点评 本题考查由三视图求几何体侧面的面积,由三视图正确复原几何体、判断出几何体的结构特征是解题的关键,考查空间想象能力.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
7.已知函数$y=\frac{1}{3}{x^3}-3x+m$的图象与x轴恰有两个公共点,则m=( )
| A. | -1或2 | B. | -9或3 | C. | -1或1 | D. | -$2\sqrt{3}$或$2\sqrt{3}$ |
