题目内容
17.如图是导函数y=f′(x)的图象,那么函数y=f(x)在区间[a,b]内极大值的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 利用函数取得极大值的充分条件即可得出.
解答 解:只有一个极大值点x2,
∵当x1<x<x2时,f′(x)>0,
当x2<x<x3时,f′(x)<0,且f′(x2)=0,
∴函数f(x)在x=x2处取得极大值.
而其它点处不满足极大值的条件,
故选:B.
点评 熟练掌握函数取得极大值的充分条件是解题的关键.

练习册系列答案
相关题目
8.两个复数z1=a1+b1i,z2=a2+b2i,(a1,b1,a2,b2都是实数且z1≠0,z2≠0),对应的向量在同一直线上的充要条件是( )
| A. | $\frac{b_1}{a_1}•\frac{b_2}{a_2}=-1$ | B. | a1a2+b1b2=0 | ||
| C. | $\frac{b_1}{a_1}=\frac{b_2}{a_2}$ | D. | a1b2=a2b1 |
5.已知函数$y=sin\frac{x}{2}+\sqrt{3}cos\frac{x}{2},x∈R$.的最大值为( )
| A. | 1+$\sqrt{3}$ | B. | 2 | C. | 1 | D. | $\sqrt{3}+\frac{1}{2}$ |
2.已知an=$\frac{n-\sqrt{2017}}{n-\sqrt{2016}}$ ( n∈N*),则在数列{an}的前100项中最小项和最大项分别是( )
| A. | a1,a100 | B. | a100,a44 | C. | a45,a44 | D. | a44,a45 |
6.($\sqrt{2}$x-1)5的展开式中第3项的系数是( )
| A. | -20$\sqrt{2}$ | B. | 20 | C. | -20 | D. | 20$\sqrt{2}$ |
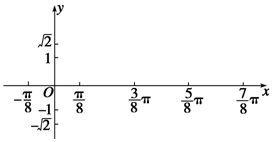 已知曲线y=Asin(ωx+φ) (A>0,ω>0)上的一个最高点的坐标为($\frac{π}{8}$,$\sqrt{2}$),此点到相邻最低点间的曲线与x轴交于点 ($\frac{3}{8}$π,0),若φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).
已知曲线y=Asin(ωx+φ) (A>0,ω>0)上的一个最高点的坐标为($\frac{π}{8}$,$\sqrt{2}$),此点到相邻最低点间的曲线与x轴交于点 ($\frac{3}{8}$π,0),若φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).