题目内容
已知三角形的三个顶点是A(-5,0),B(3,-3),C(0,2),求BC边所在的直线方程.
考点:直线的两点式方程
专题:直线与圆
分析:直接利用直线方程的两点式方程求解即可.
解答:
解:因为B(3,-3),C(0,2),
所以BC边所在的直线方程:
=
,
即5x+3y-6=0.
BC边所在的直线方程:5x+3y-6=0.
所以BC边所在的直线方程:
| y-2 |
| x-0 |
| 2+3 |
| 0-3 |
即5x+3y-6=0.
BC边所在的直线方程:5x+3y-6=0.
点评:本题考查直线方程的求法,基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若正数x,y满足3x+y=5xy,则4x+3y的最小值是( )
| A、2 | B、3 | C、4 | D、5 |
函数y=
(a>1)的图象大致形状是( )
| |x|ax |
| x |
A、 |
B、 |
C、 |
D、 |
设集合A={-1,0,1},B={x|x2-x<2},则集合A∩B=( )
| A、{-1,0,1} |
| B、{-1,0} |
| C、{0,1} |
| D、{-1,1} |
三次函数f(x)=x3+bx2+cx+d(b,c,d∈R)在区间[-1,2]上是减函数,那么b+c的取值范围是( )
A、(-∞,
| ||
B、(-∞, -
| ||
| C、A(x0,f(x0)) | ||
D、(-∞,-
|
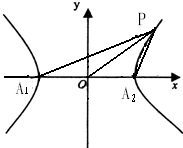 如图,P是双曲线
如图,P是双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、(0,
| ||
B、(0,
| ||
C、(0,
| ||
D、(0,
|
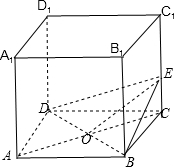 如图,正方体ABCD-A1B1C1D1,边长为1,E为CC1上一点,且EC=
如图,正方体ABCD-A1B1C1D1,边长为1,E为CC1上一点,且EC=