题目内容
若函数f（x）=x3+ax2+x-7在R上单调递增，则实数a的取值范围是 ．
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：根据函数单调递增，则等价为f′（x）≥0恒成立，利用二次函数的图象和性质即可得到结论．
解答：
解：若函数f（x）=x3+ax2+x-7在R上单调递增，
则f′（x）≥0恒成立，
即f′（x）=3x2+2ax+1≥0恒成立，
则判别式△=4a2-4×3≤0，
即a2≤3，则-
≤a≤
，
故实数a的取值范围是[-
，
]，
故答案为：[-
，
]
则f′（x）≥0恒成立，
即f′（x）=3x2+2ax+1≥0恒成立，
则判别式△=4a2-4×3≤0，
即a2≤3，则-
| 3 |
| 3 |
故实数a的取值范围是[-
| 3 |
| 3 |
故答案为：[-
| 3 |
| 3 |
点评：本题主要考查函数单调性和导数之间的关系，将函数单调递增转化为f′（x）≥0恒成立是解决本题的关键．
练习册系列答案
名校名卷单元同步训练测试题系列答案
相关题目
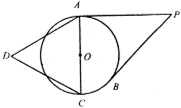如图，半径为1的圆O外有一动点P，过P作圆O的切线PA，PB切于点A，B，以直径AC为一边作正三角形△ADC，则
如图是一个平面图形的直观图，在直观图中，O′C′=O′D′=2，O′A′=3，则原平面图形的面积为若a＞b，c∈R，则下列关系一定成立的是（ ）
| A、ac2＞bc2 | ||||
| B、ac＞bc | ||||
| C、a+c＞b+c | ||||
D、
|