题目内容
4.用数学归纳法证明:当n∈N+时,1+22+33+…+nn<(n+1)n.分析 直接利用数学归纳法的证明步骤,n=1时验证不等式成立,假设n=k时不等式成立,然后证明n=k+1时,不等式也成立.
解答 证明:利用数学归纳法证明.
①当n=1时,左边=1,右边=2,左边<右边,不等式成立;
②假设n=k时,不等式成立,即1+22+33+…+kk<(k+1)k.
那么当n=k+1时,1+22+33+…+kk+(k+1)k+1<(k+1)k+(k+1)k+1=(k+1)k(1+k+1)=(k+1)k(k+2)<(k+2)k(k+2)<(k+2)k+1,
这就是说,n=k+1时,不等式也成立.
由①②可知,当n∈N+时,1+22+33+…+nn<(n+1)n.
点评 本题考查数列在不等式证明中的应用,考查数学归纳法的证明步骤,注意用上假设是证明问题的关键,是中档题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
14.已知复数z=1+$\sqrt{3}$i,则$\frac{z^2}{z-2}$=( )
| A. | 2 | B. | -2 | C. | 2i | D. | -2i |
15.已知直线m,n和平面α,若n⊥α,则“m?α”是“n⊥m”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
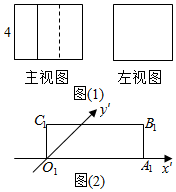 某几何体的主视图和左视图如图(1),它的俯视图的直观图是矩形O1A1B1C1如图(2),其中O1A1=6,O1C1=2,则该几何体的侧面积为( )
某几何体的主视图和左视图如图(1),它的俯视图的直观图是矩形O1A1B1C1如图(2),其中O1A1=6,O1C1=2,则该几何体的侧面积为( )