题目内容
已知函数
.
(1) 试判断函数
在
上单调性并证明你的结论；
(2) 若
恒成立, 求整数
的最大值；
(3) 求证：
.
（1）
上是减函数
（2）正整数k的最大值是3
（3）由(Ⅱ)知
∴
利用放缩法得到。
解析试题分析：解：(1)
上是减函数 4分
(2)
即h(x)的最小值大于k.
则
上单调递增,
又
存在唯一实根a, 且满足
当
∴
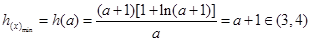故正整数k的最大值是3 ----9分
(3)由(Ⅱ)知∴
令
, 则
∴ln(1＋1×2)＋ln(1＋2×3)＋…＋ln[1＋n(n＋1)]
∴(1＋1×2)(1＋2×3)…[1＋n(n＋1)]＞e2n－3 14分
考点：导数的运用
点评：主要是考查了导数在研究函数单调性的运用，属于中档题。
练习册系列答案
相关题目
是同时符合以下性质的函数
组成的集合：
，都有
；②
上是减函数．
和
(
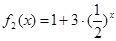)是否属于集合
,若不等式
对任意的
总成立，求实数
的取值范围．
，
.
的单调区间；
时，函数
恒成立，求实数
的取值范围；
满足
，求证：
．
是定义域为
的奇函数，且当
时，
，（
。
的值；并求函数
上是增函数。
．
.
在点（1，
）处的切线方程；
在[1，2]上是减函数，求实数a的取值范围；
是否存在实数a，当
是自然对数的底）时，函数
的最小值是3，若存在，求出a的值；若不存在，说明理由.
.
，求
的单调区间及
,求
与
的大小
,并证明你的结论.
（m为常数0＜m＜1），且数列{f（
）}是首项为2，公差为2的等差数列．
＝
时，求数列｛
；
＝
，如果｛
，函数
．
在区间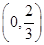
内是减函数，求实数
的取值范围；
在区间
上的最小值
；