题目内容
已知函数 ,
, .
.
(I)求函数 的单调区间;
的单调区间;
(Ⅱ)当 时,函数
时,函数 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅲ)设正实数 满足
满足 ,求证:
,求证: .
.
 当
当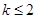 时,只有单调递增区间
时,只有单调递增区间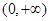 ;当
;当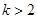 时,单调递增区间为
时,单调递增区间为 ,
,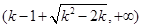 ,单调递减区间为
,单调递减区间为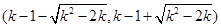 .
.
 ;
; 详见解析.
详见解析.
解析试题分析: 先求出
先求出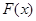 的导数,讨论
的导数,讨论 ,利用导数的正负与函数单调性得关系求出单调区间;
,利用导数的正负与函数单调性得关系求出单调区间; 当x>1时,函数f(x)>g(x)恒成立转化为
当x>1时,函数f(x)>g(x)恒成立转化为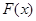 >0恒成立.结合第
>0恒成立.结合第 问讨论的单调区间得出
问讨论的单调区间得出 的范围;
的范围;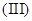 结合第
结合第 问,令
问,令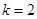 ,
,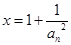 ,所以
,所以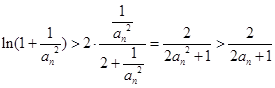 ,再利用柯西不等式,
,再利用柯西不等式,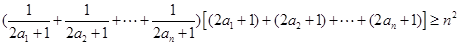 ,其中由条件
,其中由条件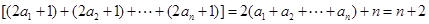 .最后得证.
.最后得证.
试题解析:(Ⅰ)易知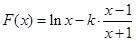 ,定义域是
,定义域是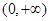 .
.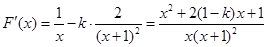 1分
1分
由 的判别式
的判别式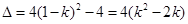
①当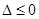 即
即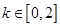 时,
时,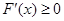 恒成立,则
恒成立,则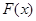 在
在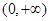 单调递增 2分
单调递增 2分
②当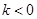 时,
时,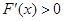 在
在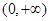 恒成立,则
恒成立,则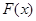 在
在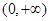 单调递增 3分
单调递增 3分
③当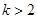 时,方程
时,方程 的两正根为
的两正根为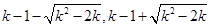
则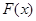 在
在 单调递增,
单调递增,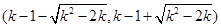 单调递减,
单调递减,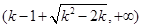 单调递增
单调递增
综上,当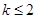 时,只有单调递增区间
时,只有单调递增区间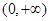
当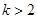 时,单调递增区间为
时,单调递增区间为 ,
,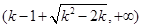
单调递减区间为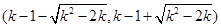 5分
5分
(Ⅱ)即 时,
时,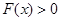 恒成立
恒成立
当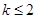 时,
时,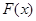 在
在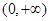 单调递增 ∴当
单调递增 ∴当 时,
时,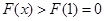 满足条件 7分
满足条件 7分
当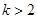 时,
时,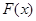 在
在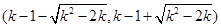 单调递减
单调递减
则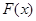 在
在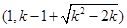 单调递减
单调递减
此时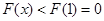 不满足条件
不满足条件
故实数 的取值范围为
的取值范围为 9分
9分
(Ⅲ)由(2)知,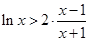 在
在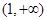 恒成立
恒成立
令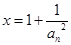 则
则  10分
10分
∴ 11分
11分
又
其中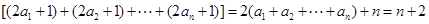
∴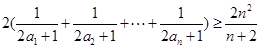 &nb
&nb

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为 平方米,且高度不低于
平方米,且高度不低于 米.记防洪堤横断面的腰长为
米.记防洪堤横断面的腰长为 (米),外周长(梯形的上底线段
(米),外周长(梯形的上底线段 与两腰长的和)为
与两腰长的和)为 (米).
(米).
 米,则其腰长
米,则其腰长
 的解集为
的解集为 ,求实数
,求实数 的值;
的值; 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 的奇函数
的奇函数 满足
满足 ,且当
,且当 时,
时,  .
. 上的解析式;
上的解析式; 取何值时,方程
取何值时,方程 在
在 上有解?
上有解? ,
,
 .
. 的解集;
的解集; 的不等式
的不等式 在
在 的取值范围.
的取值范围.
 >
> 成立,则称函数
成立,则称函数 lnx是J函数时,求m的取值范围;
lnx是J函数时,求m的取值范围; g(1)的大小;
g(1)的大小; .
. 在
在
 上单调性并证明你的结论;
上单调性并证明你的结论; 恒成立, 求整数
恒成立, 求整数 的最大值;
的最大值; .
.
 的奇偶性;
的奇偶性; 上是增函数还是减函数?证明你的结论.
上是增函数还是减函数?证明你的结论.