题目内容
函数f（x）=lnx+x-6的零点所在区间为（ ）
| A、（2，3） |
| B、（3，4） |
| C、（4，5） |
| D、（5，6） |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：据函数零点的判定定理，判断f（2），f（3），f（4），f（5），f（6）的符号，即可求得结论．
解答：
解：∵f（2）=2+ln2-6＜0，
f（3）=4+ln3-6＜0，
f（4）=4+ln4-6＜0，
f（5）=5+ln5-6＞0，
f（6）=6+ln6-6＞0，
∴f（4）•f（5）＜0，
∴函数f（x）=lnx+x-6的零点所在区间为（4，5）．
故选C．
f（3）=4+ln3-6＜0，
f（4）=4+ln4-6＜0，
f（5）=5+ln5-6＞0，
f（6）=6+ln6-6＞0，
∴f（4）•f（5）＜0，
∴函数f（x）=lnx+x-6的零点所在区间为（4，5）．
故选C．
点评：考查函数的零点的判定定理，以及学生的计算能力．解答关键是熟悉函数的零点存在性定理，此题是基础题．
练习册系列答案
口算能手系列答案
相关题目
已知：集合P={x|x=sin
，k∈Z}，集合Q={y|y=sin
，k∈Z}，则P与Q的关系是（ ）
| (k-3)π |
| 3 |
| (-21-k)π |
| 3 |
| A、P?Q | B、P?Q |
| C、P=Q | D、P∩Q=∅ |
已知定义在R上的函数f（x），其导函数y=f′（x）的大致图象如图所示，则下列叙述正确的是（ ）| A、f（a）取得极小值 |
| B、f（d）取得最小值 |
| C、f（x）在（a，c）上单调递增 |
| D、f（e）取得极大值 |
直线
（t为参数）与曲线ρ=1的位置关系是（ ）
|
| A、相离 | B、相交 | C、相切 | D、不确定 |
函数f（x）=sin（4x+φ），x∈[0，2π]的一个零点为
，则f（x）的所有极值点的和为（ ）
| π |
| 8 |
| A、7π | ||
B、
| ||
C、
| ||
| D、9π |
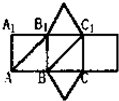如图，正三棱柱的平面展开图，各侧面都是正方形，在这个正三棱柱中：