Question

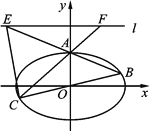
【题目】如图所示的钢板的边界是抛物线的一部分，且垂直于抛物线对称轴，现欲从钢板上截取一块以为下底边的等腰梯形钢板，其中均在抛物线弧上.设（米），且.

（1）当时，求等腰梯形钢板的面积;

（2）当为何值时，等腰梯形钢板的面积最大？并求出最大值.

Answer 1

【答案】见解析

【解析】如图，以所在的直线为轴，抛物线的对称轴为轴，一米为长度单位，建立如图所示的平面直角坐标系.依题意，.

设经过三点的抛物线的方程为，

因为抛物线经过点，所以，

于是经过三点的曲线的方程为.……………4分

（1）由题意得:,.……………6分

（2）因为（米），所以点，

从而等腰梯形钢板的面积.……………8分

所以.

令得，，

列表：

	+	0	-
	↗	极大值	↘

所以当时，取得最大值.……………12分

答：（1）当时，等腰梯形钢板的面积为平方米.

（2）当时，等腰梯形钢板的面积最大，最大值为平方米. ……………14分