题目内容
已知集合P={x|1≤x≤8,x∈Z},直线y=2x+1与双曲线mx2-ny2=1有且只有一个公共点,其中m、n∈P,则满足上述条件的双曲线共有 个.
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:依题意,将直线y=2x+1与双曲线mx2-ny2=1的方程联立,消去y得:(m-4n)x2-4nx-n-1=0;分①直线y=2x+1与双曲线mx2-ny2=1相切,②直线y=2x+1与双曲线mx2-ny2=1相交,讨论,分别利用判别式与直线y=2x+1与双曲线mx2-ny2=1的一条渐近线平行即可求得答案.
解答:
解:∵直线y=2x+1与双曲线mx2-ny2=1有且只有一个公共点,
∴由直线y=2x+1与双曲线mx2-ny2=1消去y得:(m-4n)x2-4nx-n-1=0,
①若m-4n≠0,直线y=2x+1与双曲线mx2-ny2=1相切,
则△=16n2-4(m-4n)(-n-1)=0,
整理得:m(n+1)=4n,
∴m=
,
又m,n∈P={x|1≤x≤8,x∈Z},
∴当n=1时,m=2符合题意;当n=3时,m=3符合题意;当n为2,4,5,…,8时均不符合题意;
②若m-4n=0,直线y=2x+1必与双曲线mx2-ny2=1的一条渐近线y=
x平行,
∵m,n∈P,
∴当n=1时,m=4;当n=2时,m=8.
综合①②知,满足上述条件的双曲线共有4条,
故答案为:4.
∴由直线y=2x+1与双曲线mx2-ny2=1消去y得:(m-4n)x2-4nx-n-1=0,
①若m-4n≠0,直线y=2x+1与双曲线mx2-ny2=1相切,
则△=16n2-4(m-4n)(-n-1)=0,
整理得:m(n+1)=4n,
∴m=
| 4n |
| n+1 |
又m,n∈P={x|1≤x≤8,x∈Z},
∴当n=1时,m=2符合题意;当n=3时,m=3符合题意;当n为2,4,5,…,8时均不符合题意;
②若m-4n=0,直线y=2x+1必与双曲线mx2-ny2=1的一条渐近线y=
|
∵m,n∈P,
∴当n=1时,m=4;当n=2时,m=8.
综合①②知,满足上述条件的双曲线共有4条,
故答案为:4.
点评:本题考查直线与圆锥曲线的位置关系,考查方程思想与分类讨论思想的综合应用,考查双曲线的渐近线方程,考查综合运算与求解能力,属于难题.

练习册系列答案
相关题目
函数y=2x3-ax+c在(-∞,+∞)上单调递增,则( )
| A、a≤0,c∈R |
| B、a≥0,c∈R |
| C、a<0,c=0 |
| D、a≤0,c≠0 |
已知(5x-3)n的展开式中各项系数的和比(x-y-
)2n的展开式中各项系数的和多1023,则n的值为( )
| 1 |
| y |
| A、9 | B、10 | C、11 | D、12 |
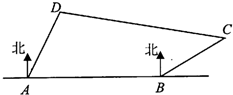 如图,海岸线上有相距10海里的两座灯塔A、B,灯塔B位于灯塔A的正东方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏东30°方向,与A相距5海里的D处;乙船位于灯塔B的北偏东60°方向,与B相距3
如图,海岸线上有相距10海里的两座灯塔A、B,灯塔B位于灯塔A的正东方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏东30°方向,与A相距5海里的D处;乙船位于灯塔B的北偏东60°方向,与B相距3