题目内容
4.函数f(x)满足条件:①定义域为R,且对任意x∈R,f(x)<1;②对任意小于1的正实数a,存在x0,使f(x0)=f(-x0)>a,则f(x)可能是( )| A. | $\frac{|x|+1}{|x|-1}$ | B. | $\frac{{x}^{2}}{{x}^{2}+1}$ | C. | $\frac{x}{\sqrt{{x}^{2}+1}}$ | D. | $\frac{x+1}{{x}^{2}+1}$ |
分析 根据题意,对选项中的四个函数进行判断,得出符合条件的函数即可.
解答 解:对于A,y=f(x)=$\frac{|x|+1}{|x|-1}$(x≠±1)不满足定义域为R,∴是不可能的函数;
对于B,y=f(x)=$\frac{{x}^{2}}{{x}^{2}+1}$(x∈R),对任意x∈R,f(x)<1;
且对任意小于1的正实数a,存在x0,使f(x0)=f(-x0)>a,∴是可能的函数;
对于C,y=f(x)=$\frac{x}{\sqrt{{x}^{2}+1}}$,不满足f(x)=f(-x),∴是不可能的函数;
对于D,y=f(x)=$\frac{x+1}{{x}^{2}+1}$,当x=0时,f(0)=1,不满足x∈R时f(x)<1,∴是不可能的函数.
故选:B.
点评 本题考查了函数的定义与性质的应用问题,属于新定义的函数的应用问题,是易错题目.

练习册系列答案
相关题目
12.已知数列{an}(an>1)满足an+1=10an2,数列{bn}满足bn=lgan+1,且4b1为bm与bk的等比中项(m,k∈N*),则$\frac{1}{m}+\frac{1}{k}$的最小值是( )
| A. | $\frac{25}{6}$ | B. | 2 | C. | $\frac{7}{3}$ | D. | $\frac{2}{3}$ |
9.设全集U=R,集合M={x|ln(1-x)<0},N={x|$\frac{\sqrt{2}}{2}$<2x<4},则(∁UM)∩N=( )
| A. | {x|-$\frac{1}{2}$<x≤0} | B. | {x|-$\frac{1}{2}$<x≤0或1≤x<2} | C. | {x|-1<x≤0} | D. | {x|-1<x≤0或1≤x<2} |
20.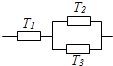 三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2},\frac{3}{4},\frac{3}{4}$且是互相独立的,按图种方式接入电路,电路正常工作的概率是( )
三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2},\frac{3}{4},\frac{3}{4}$且是互相独立的,按图种方式接入电路,电路正常工作的概率是( )
 三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2},\frac{3}{4},\frac{3}{4}$且是互相独立的,按图种方式接入电路,电路正常工作的概率是( )
三个元件T1,T2,T3正常工作的概率分别为$\frac{1}{2},\frac{3}{4},\frac{3}{4}$且是互相独立的,按图种方式接入电路,电路正常工作的概率是( )| A. | $\frac{7}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{15}{32}$ | D. | $\frac{17}{32}$ |
 如图,点A在半径为1且圆心在原点的圆上,∠A0x=45°,点P从点A出发,依逆时针方向匀速地沿单位圆周旋转.已知P在1s内转过的角度为θ(0°<θ<180°),经过2s到达第三象限,经过14s后又回到出发点A.求θ,并判断其所在的象限.
如图,点A在半径为1且圆心在原点的圆上,∠A0x=45°,点P从点A出发,依逆时针方向匀速地沿单位圆周旋转.已知P在1s内转过的角度为θ(0°<θ<180°),经过2s到达第三象限,经过14s后又回到出发点A.求θ,并判断其所在的象限.