题目内容
18.在直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}{x=t}\\{y=4-t}\end{array}\right.$(t为参数),在以O为极点x轴的非负半轴为极轴建立的极坐标系中,曲线C的极坐标方程为ρ=2.(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若点Q是曲线C上的动点,求点Q到直线l的距离的最大值.
分析 (1)利用三种方程的转化方法,求直线l的普通方程和曲线C的直角坐标方程;
(2)由于点Q是曲线C上的点,则可设点Q的坐标为(2cosθ,2sinθ),点Q到直线l的距离为d=$\frac{|2sin(θ+45°)-4|}{\sqrt{2}}$.利用三角函数的单调性值域即可得出.
解答 解:(1)由直线l的参数方程为$\left\{\begin{array}{l}{x=t}\\{y=4-t}\end{array}\right.$(t为参数),可直线l的普通方程为x+y-4=0.
由ρ=2,得曲线C的直角坐标方程为x2+y2=4.
(2)由于点Q是曲线C上的点,则可设点Q的坐标为(2cosθ,2sinθ),
点Q到直线l的距离为d=$\frac{|2sin(θ+45°)-4|}{\sqrt{2}}$.
当sin(θ+45°)=-1时,点Q到直线l的距离的最大值为3$\sqrt{2}$.
点评 本题考查了直角坐标与极坐标的互化、参数方程化为普通方程及其应用、三角函数的和差公式及其单调性、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
8.已知抛物线x2=4y的焦点为F,准线为l,抛物线的对称轴与准线交于点Q,P为抛物线上的动点,|PF|=m|PQ|,当m最小时,点P恰好在以F,Q为焦点的椭圆上,则椭圆的离心率为( )
| A. | $3-2\sqrt{2}$ | B. | $2-\sqrt{2}$ | C. | $\sqrt{3}-\sqrt{2}$ | D. | $\sqrt{2}-1$ |
6.在复平面内,复数z=$\frac{2i}{1+i}$(i为虚数单位)对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.已知函数f(x)=-x2-6x-3,g(x)=2x3+3x2-12x+9,m<-2,若?x1∈[m,-2),?x2∈(0,+∞),使得f(x1)=g(x2)成立,则m的最小值为( )
| A. | -5 | B. | -4 | C. | -2$\sqrt{5}$ | D. | -3 |
7.设M、N是直线x+y-2=0上的两动点,且|MN|=$\sqrt{2}$,则$\overrightarrow{OM}$•$\overrightarrow{ON}$的最小值为( )
| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{3}{2}$ |
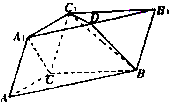 在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D为A1B1的中点.
在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D为A1B1的中点.