题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,且cos(A-B)cos B-sin(A-B)sin(A+C)
=-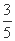 .
.
(1)求sin A的值;
(2)若a=4 ,b=5,求向量
,b=5,求向量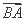 在
在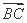 方向上的投影.
方向上的投影.
解:(1)由cos(A-B)cos B-sin(A-B)sin(A+C)=-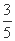 ,
,
得cos(A-B)cos B-sin(A-B)sin B=-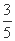 .
.
则cos(A-B+B)=- 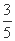 ,
,
即cos A=-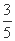 .
.
又0<A<π,则sin A= .
.
(2)由正弦定理,有 =
= ,
,
所以sin B= =
=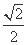 .
.
由题知a>b,则A>B,故B= .
.
根据余弦定理,有(4 )2=52+c2-2×5c×
)2=52+c2-2×5c× ,解得c=1或c=-7(负值舍去).
,解得c=1或c=-7(负值舍去).
故向量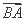 在
在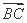 方向上的投影为|
方向上的投影为|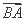 |cos B=
|cos B=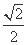 .
.

练习册系列答案
相关题目
 (x>0,a>0)在x=3时取得最小值,则a= .
(x>0,a>0)在x=3时取得最小值,则a= . 
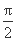 时,f(x)取得最大值,则( )
时,f(x)取得最大值,则( )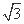 ,1),其中θ∈(0,
,1),其中θ∈(0, 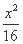 -
-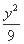 =1的离心率为 .
=1的离心率为 .  +
+ =1(a>b>0)的左、右焦点,P为直线x=
=1(a>b>0)的左、右焦点,P为直线x= 上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( ) (B)
(B) (C)
(C) (D)
(D) 