题目内容
11.已知函数f(x)=(ax2-bx)ex(其中e是自然对数的底数,a,b∈R)的图象在A(0,f(0))处的切线与直线x+y+2=0垂直.(Ⅰ)当a=-$\frac{1}{2}$时,求函数f(x)的极值点;
(Ⅱ)若f(x)≤x在[-1,0]上恒成立,求实数a的取值范围.
分析 (Ⅰ)求出函数的导数,根据f′(0)=1,求出b的值;求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出f(x)的极值点即可;
(Ⅱ)问题转化为a≤$\frac{{e}^{-x}-1}{x}$在[-1,0]恒成立,令g(x)=$\frac{{e}^{-x}-1}{x}$,x∈[-1,0],根据函数的单调性求出a的范围即可.
解答 解:(Ⅰ)f′(x)=[ax2+(2a-b)x-b]ex,
故k=f′(0)=-b=1,解得:b=-1,
故f(x)=(ax2+x)ex,
a=-$\frac{1}{2}$时,f(x)=(-$\frac{1}{2}$x2+x)ex,
f′(x)=(-$\frac{1}{2}$x2+1)ex,
令f′(x)>0,解得:-$\sqrt{2}$<x<$\sqrt{2}$,
令f′(x)<0,解得:x>$\sqrt{2}$或x<-$\sqrt{2}$,
故f(x)在(-∞,-$\sqrt{2}$)递减,在(-$\sqrt{2}$,$\sqrt{2}$)递增,在($\sqrt{2}$,+∞)递减,
故x=-$\sqrt{2}$是f(x)的极小值点,x=$\sqrt{2}$是f(x)的极大值点;
(Ⅱ)若f(x)≤x在[-1,0]上恒成立,
即(ax2+x)ex≤x在[-1,0]恒成立,
问题转化为a≤$\frac{{e}^{-x}-1}{x}$在[-1,0]恒成立,
令g(x)=$\frac{{e}^{-x}-1}{x}$,x∈[-1,0],
g′(x)=$\frac{{-e}^{-x}(x+1)-1}{{x}^{2}}$<0,
故g(x)在[-1,0]递减,
而x→0时,$\underset{lim}{x→0}$$\frac{{e}^{-x}-1}{x}$=$\underset{lim}{x→0}$$\frac{{-e}^{-x}}{1}$=-1,
故a≤-1.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,考查转化思想,是一道综合题.

| A. | [-1,$\frac{1}{2}$] | B. | (-∞,-1]∪[$\frac{1}{2}$,+∞) | C. | [0,$\frac{4}{3}$] | D. | (-∞,-2]∪[$\frac{4}{3}$,+∞) |
| A. | 1-2i | B. | 1+2i | C. | -1-2i | D. | -1+2i |
| A. | 向左平行移动$\frac{π}{12}$个单位长度 | B. | 向右平行移动$\frac{π}{12}$个单位长度 | ||
| C. | 向左平行移动$\frac{π}{6}$个单位长度 | D. | 向右平行移动$\frac{π}{6}$个单位长度 |




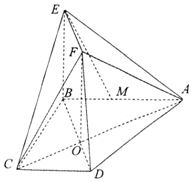 如图所示,直角梯形ABCD两条对角线AC,BD的交点为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,M为线段AB上一点,AM=2MB,且AB⊥BC,AB∥CD,AB=BE=6,CD=BC=3.
如图所示,直角梯形ABCD两条对角线AC,BD的交点为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,M为线段AB上一点,AM=2MB,且AB⊥BC,AB∥CD,AB=BE=6,CD=BC=3.