题目内容
若f（x）是奇函数，且在（0，+∞）内是减函数，又有f（-2）=0，则x•f（x）＜0的解集是 ．
考点：奇偶性与单调性的综合
专题：函数的性质及应用
分析：根据函数奇偶性和单调性之间的关系，利用数形结合即可得到结论．
解答：
解：∵奇函数在（0，+∞）上是减函数，
∴在（-∞，0）上也是减函数，
且f（-2）=-f（2）=0，即f（2）=0，
作出函数f（x）的草图：
则不等式x•f（x）＜0等价为x＞0时，f（x）＜0，此时x＞2
当x＜0时，f（x）＞0，此时x＜-2，
综上不等式的解为x＞2或x＜-2，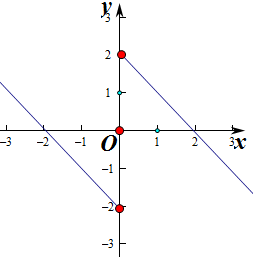
故不等式的解集为（-∞，-2）∪（2，+∞），
故答案为：（-∞，-2）∪（2，+∞）
∴在（-∞，0）上也是减函数，
且f（-2）=-f（2）=0，即f（2）=0，
作出函数f（x）的草图：
则不等式x•f（x）＜0等价为x＞0时，f（x）＜0，此时x＞2
当x＜0时，f（x）＞0，此时x＜-2，
综上不等式的解为x＞2或x＜-2，
故不等式的解集为（-∞，-2）∪（2，+∞），
故答案为：（-∞，-2）∪（2，+∞）
点评：本题主要考查不等式的解法，利用函数的奇偶性和单调性之间的关系是解决本题的关键，综合考查函数性质的应用．
练习册系列答案
相关题目
已知命题p：“若直线ax+y+1=0与直线ax-y+2=0垂直，则a=1”；命题q：“a
＜b
”是“a＜b”的充要条件，则（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、p真，q假 |
| B、“p∧q”真 |
| C、“p∨q”真 |
| D、“p∨q”假 |
设等差数列{an}的公差为d，且a3=2，若数列{2 a1an}为递增数列，则公差d的取值范围是（ ）
| A、d＜0 | B、d＞1 |
| C、d＞1或d＜0 | D、0＜d＜1 |
将函数f（x）=cos2x的图象向右平移
个单位后得到函数g（x），则g（x）具有性质（ ）
| π |
| 4 |
A、最大值为a，图象关于直线x=
| ||||
B、在（0，
| ||||
C、在（-
| ||||
D、周期为π，图象关于点（
|
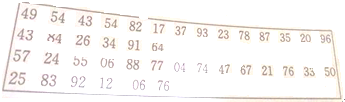福利彩票“双色球”中，红球号码有编号为01，02，…，33的33个个体组成，某彩民利用下面的随机数表选取6组数作为6个红球的编号，选取方法是从随机数表第1行的第6列和第7列数字开始由左到右依次选取两个数字，则选出来的第6个红球的编号为（ ）| A、23 | B、09 | C、02 | D、17 |
已知两个单位向量
，
的夹角为60°，
=（1-t）
+t
，若
•
=-
，则实数t的取值是（ ）
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| 1 |
| 2 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|