题目内容
如果cos(π+A)=-
,那么sin(
-A)= .
| 1 |
| 2 |
| π |
| 2 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:已知等式利用诱导公式化简求出cosA的值,所求式子利用诱导公式化简后将cosA的值代入计算即可求出值.
解答:
解:∵cos(π+A)=-cosA=-
,即cosA=
,
∴sin(
-A)=cosA=
.
故答案为:
| 1 |
| 2 |
| 1 |
| 2 |
∴sin(
| π |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
相关题目
设全集I=R,M={x|x2>4},N={x|1<x<3},则(CIM)∩N为( )
| A、{x|x<2} |
| B、{x|1<x≤2} |
| C、{x|-2≤x<1} |
| D、{x|-2≤x≤2} |
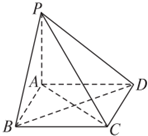 已知PA垂直于正方形ABCD所在平面,连接PB、PC、PD、AC、BD,则下列垂直关系中正确的序号是
已知PA垂直于正方形ABCD所在平面,连接PB、PC、PD、AC、BD,则下列垂直关系中正确的序号是